|
即分子先绕轴旋转120度,再转240度,共转360度等于恒等元素;分子绕轴转240度,再转240度,等于绕轴转动480度,扣去360度,相当于绕轴转动120度。──满足封闭性
|
|
②群中存在恒等元素E。 |
③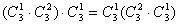 ,乘法结合律成立。 ,乘法结合律成立。 |
④因为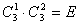 ,所以 ,所以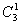 与 与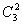 互为逆元素,则四个条件都满足,所以 互为逆元素,则四个条件都满足,所以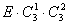 三个元素组成一个 三个元素组成一个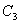 群。 群。
|
| 2.群的乘法
|
仍以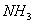 为例。实际上 为例。实际上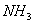 除了存在 除了存在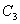 轴外,还存在经过 轴外,还存在经过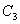 轴与 轴与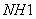 键的 键的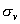 平面。通过平面反映,可将 平面。通过平面反映,可将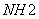 键反映到 键反映到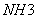 键,同理还有经过 键,同理还有经过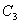 轴与 轴与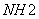 键的 键的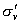 平面,经过 平面,经过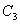 轴与 轴与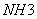 的 的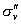 ,共有三个垂直平面,相交于 ,共有三个垂直平面,相交于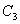 轴,现在我们来做它的乘法表。 轴,现在我们来做它的乘法表。
|
①首先,根据恒等元素与任何元素相乘,等于它本身可写出第一行与第一列,再根据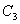 群中的结果可写出乘法表左上角的结果。 群中的结果可写出乘法表左上角的结果。 |
|
|
②第二步,进行右上角的乘法,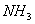 分子进行 分子进行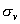 反映,N和H1保持不变,H2与H3互换位置,再绕 反映,N和H1保持不变,H2与H3互换位置,再绕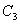 轴旋转120度,则N还是不变,H2到H1位置,H1到H2位置,H3回到原位置,两个操作的净结果,相当于一个 轴旋转120度,则N还是不变,H2到H1位置,H1到H2位置,H3回到原位置,两个操作的净结果,相当于一个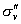 平面反映……可写出右上角的九个结果。 平面反映……可写出右上角的九个结果。 |
|
③同理也可写出左下角的九个结果。 |
|
|
④最后1/4乘法表是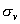 平面相乘,每个平面与自己相乘的结果是恒等元素, 平面相乘,每个平面与自己相乘的结果是恒等元素,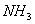 分子进行 分子进行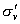 反映,则N原子保持不变。H3还在H1的位置,H2到了H3的位置,H1到了H2的位置,净结果相当于一个 反映,则N原子保持不变。H3还在H1的位置,H2到了H3的位置,H1到了H2的位置,净结果相当于一个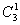 的旋转。 的旋转。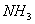 分子先进行 分子先进行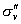 反映,再进行 反映,再进行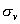 反映,净结果相当于分子旋转240度( 反映,净结果相当于分子旋转240度(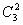 )。……同理可得到 )。……同理可得到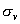 平面相乘结果都是旋转 平面相乘结果都是旋转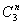 。这样,我们做出了 。这样,我们做出了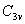 点群的乘法表 点群的乘法表
|
|
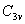 点群的乘法表 点群的乘法表
|
|
|
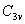 点群共有六个元素,六个元素相乘所得结果还在这六个元素之中,满足封闭性,又有恒等元素E, 点群共有六个元素,六个元素相乘所得结果还在这六个元素之中,满足封闭性,又有恒等元素E,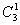 与 与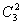 元素互为逆元素,三个 元素互为逆元素,三个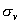 元素与自身为逆元素,还满足乘法结合律,符合群的条件。 元素与自身为逆元素,还满足乘法结合律,符合群的条件。
|
| 3.群的一些相关概念
|
| (1)群的分类:群有各种类型,如旋转群,置换群,点群,空间群,李群……
|
| 本章介绍的是研究分子对称性的对称点群,本课程在介绍晶体结构时要介绍空间群,对称点群的特点是所有的对称元素交于一点。
|
(2)群阶:群所含的对称元素个数称为群阶,如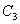 群群阶为3, 群群阶为3,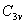 群群阶为6。 群群阶为6。
|
(3)类:群中某些对称元素在相似变换中互为共轭元素的可分为一类。如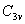 点群中的元素可分为三类,E元素成一类, 点群中的元素可分为三类,E元素成一类,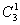 与 与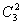 旋转成一类。三个 旋转成一类。三个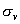 平面而成一类。 平面而成一类。 |
(4)子群:在一些较大的群中可以找到一些较小的群,称为子群。例如: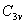 群中有子群 群中有子群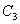 。子群也要满足群的四个要求。 。子群也要满足群的四个要求。 |