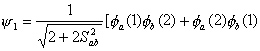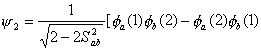|
|
|||||||||||||||||||||
|
|
||||||||||||||||||||||
| 当前位置 ->§ 4 双原子分子 -> 4.4 价键理论和氢分子结构
-> 4.4.2 氢分子的价键处理 |
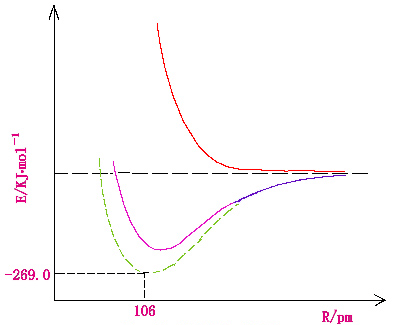
| 二、氢分子的价键处理 三十年代Heitler-London对H2的变分处理是价键理论的开创性工作。H2分子有两个原子核A、B和两个电子,如图4-5 所示,当两个核远离时,体系的基态就是两个氢原子。我们可以假定电子e1和核A相结合,电子e2和核B相结合,两个原子间的相互作用能是核间距rAB的函数,当rAB不断缩小时,它迅速地变为强烈的排斥作用(参见图4-5中的虚线)
图4-3 H2+的能量曲线图 从计算看,这两个原子不会结合成稳定的分子。但是这里我们忽略了另一种结构,即电子e2和核A的结合、电子e1和核B的结合,与上面假定的结构有相同的稳定性。根据量子力学原理,我们不该认为其中某一结构可单独来描述这个体系的基态,我们要采用两种结构的组合来反映这一体系。
这样得出来的相互作用能曲线具有明显的极小值(上图下面的实线)我们用
为变分试探函数。 氢分子的哈密顿算符可表示为两个电子的动能,电子与核的吸引能,电子与电子排斥能,核与核排斥能之和。
= 再把它们组合成Ha原子哈密顿算符,Hb原子哈密顿算符和其它相互作用势 根据变分法
这样计算所得的键能约为实验测定值的67%,以后有人进一步改进试探波函数,计算得到的键能达正确值的80%。Pauling 分析以上的处理,认为只考虑氢分子的两个电子在运动中分别靠近不同的核的结构,未考虑两个电子同时靠近某个核的情况,即离子结构III、IV: 结构III:
(HA:)-H 这类结构包含一个正氢离子H+和一个具有氢电子结构的负氢离子H-。在负离子中也满足了电子配对的要求,III、IV结构在基态氢分子中也占有一定比例。 计算表明,考虑这两种结构的能量约占总键能的5%。Pauling
认为,实验键能中余下的15%可能是由分子变形作用引起的,在前面简单处理中忽略了复杂的相互作用,直至1958年James
等对基态H2作了精确的理论处理,获得的分子键能为102.62Kcal/mol,与实验测定一致;平衡核间距,振动频率等也与实验相符。
|
|||||||||||||||||