|
原子轨道波函数 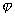 可表示为径向函数与球谐函数的乘积:
可表示为径向函数与球谐函数的乘积:
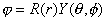
在转动作用下,径向分布函数保持不变,仅与角量子数 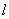 、球谐函数
、球谐函数 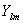 有关,某一
有关,某一 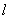 值的球谐函数在转动下产生的表示
值的球谐函数在转动下产生的表示 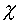 是所有的分量值的加和:
是所有的分量值的加和:
转动角度为 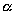 的对称操作作用在角量子数为
的对称操作作用在角量子数为 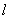 的球谐函数上,产生的表示:
的球谐函数上,产生的表示:
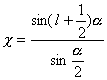 (
( 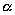
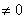 )
)
在不同对称性的配体场中,这些轨道函数可分裂为不同不可约表示的基,现以 O群对称性场为例说明:
当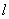 =0时,即 s轨道: =0时,即 s轨道:
|
|
|
| 无论转动多大角度,值恒为 1, s轨道的可约表示与 O群中 A1不可约表示完全相同。
|
表6-1旋转群表示基向点群不可约表示分解
|
当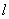 =1时,即 p轨道,在恒等元素 E作用下, 3个 p分量保持不变,在 C4(转动1/2)作用下: =1时,即 p轨道,在恒等元素 E作用下, 3个 p分量保持不变,在 C4(转动1/2)作用下:
|
在 C3(转动为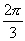 )作用下: )作用下:
|
|
|
|
在 C2(转动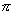 )作用下: )作用下:
|
|
|
|
|
得到的可约表示与
T1不可约表示完全相同,
即 p轨道可作为 O群 T1不可约表示的基函数
当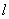 =2时, d规道在恒等元素 E作用下,仍有 5个分量, =2时, d规道在恒等元素 E作用下,仍有 5个分量,
|
| 在 C4作用下:
|
|
|
| 在 C3作用下:
|
|
|
| 在 C2作用下:
|
|
|
| |
| |
将可约表示 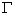 d代入公式
d代入公式
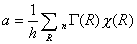
在 O群中可分解为 E和 T2表示的直和
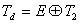
E为二重简并, T2为三重简并,即 d轨道可分裂为 E和 T2二个能级。
当 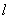 =3时, f轨道也可得到一组可约表示,(见 O群特征标表)进行再约化,可约表示向不可约表示约化,可得
=3时, f轨道也可得到一组可约表示,(见 O群特征标表)进行再约化,可约表示向不可约表示约化,可得
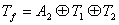 ,即 f轨道在 O群作用下可分解成 A2、 T1和 T2三个不可约表示的直和。
,即 f轨道在 O群作用下可分解成 A2、 T1和 T2三个不可约表示的直和。
同理, g轨道可分解为 A1, E, T1和 T2 四个不可约表示的直和。
以上为各种原子轨道在 O群(八面体场)对称元素作用下进行的群分解,用相同方法,我们也可以得到各种原子轨道在 D4h(四方形场)、 Td(四面体场)、 D3d(三角场)等不同对称群作用下的轨道能级分裂。
例如 d轨道在 Oh(八面体场)作用下,可分裂为 Eg和 T2g两个能级, T2g能级较低,在 Td(四面体场)作用下,也分裂为 E和 T2两个能级,但 E能级较低,在 D4h(正方形)中, d轨道分裂为 A1g(dz2)、 B1g(dx2-y2)和 Eg(dxy,dzy)四个能级,其中 A1g能级最低,Eg其次, B2g再次, B1g最高。
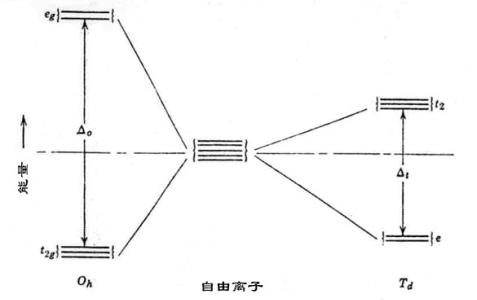
图6-12
表示一组d 轨道被八面体和四面体环境分裂后,得到e
和t2轨道的相对能量图
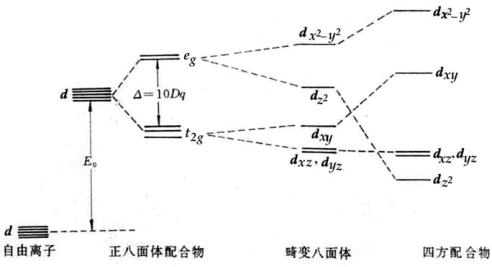
图6-13
正八面体场中的d 电子能级 |