|
当配体与中心离子间的作用很强,大于中心离子价电子间的作用时,我们处理配合物分子轨道时,先考虑配体场对中心离子
d电子的影响,再考虑
d电子间的相互作用,这样处理称之为强场方案。
中心离子的 d轨道在八面体场 (Oh)分裂成 Eg和 T2g两个能级,我们以 d2为例说明。两个 d电子填充在两个能级不同的轨道上有 3种可能: 1.两个电子都填充在能量较低 t2g轨道上, 2.一个填在 t2g,另一个填在 eg上, 3.两个都填在能量较高的 eg轨道上,即:
|
|
|
|
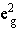 |
|
(1)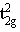 : (由于 Oh场中都是对称表示,以下略去 g下标 ) : (由于 Oh场中都是对称表示,以下略去 g下标 )
|
|
t2是三重简并的轨道,每个电子又可以自旋向上,自旋向下两种方式填入这三个轨道,即有六种选择。两个电子在六种选择中填充,有共 15种状态。两个电子填充在 t2轨道上,它们以某种方式偶合,该状态可用两个单电子不可约表示的直积来表示。即以两个 t2不可约表示的特征标相乘,得到一个可约表示,再用以下公式将可约表示分解为不可约表示的直和。
|
|
|
|
|
|
还要进一步确定这些谱项的多重性, A1为一种状态, E为二重简并状态, T1、 T2为三重简并,若每个都是单态,又包含 9种状态,还应有 1个三重简并的三重态,或( A1+E)是三重态,我们参考一下弱场方案的谱项,可定出 T1为三重态,即 1A+1E+3T1+1T2
|
|
(2)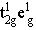 : :
|
|
对于 1个电子填在 t2g轨道有 6种选择, 1个电子填在 eg轨道有 4种选择,合起来共有 24种状态:
|
|
|
|
t2与 e不可约表示的直积为一可约表示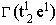 ,再进行群分解,可得到 2个 t1和 2个 t2四个不可约表示的直和,若都是单态,仅有 12个状态,故应是 2个单态 2个三重态,即 1T1+1T2+3T1+3T2 ,再进行群分解,可得到 2个 t1和 2个 t2四个不可约表示的直和,若都是单态,仅有 12个状态,故应是 2个单态 2个三重态,即 1T1+1T2+3T1+3T2
|
|
(3)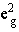 : :
|
|
一个电子填在 eg轨道有 4种选择, 2个电子填在 eg轨道 (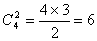 ),有 6种选择,即 ),有 6种选择,即
|
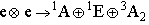 这样,我们得到了 d2组态在强场中先分成
这样,我们得到了 d2组态在强场中先分成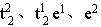 3种情况,然后对 3种情况的状态用点群不可约表示直积处理,最后群分解,得到 3种情况中 2个电子相互作用产生的谱项能级分裂,将这些结果画在图的右边,与弱场的左图联系起来,得到 d2离子在八面体场中的能级相关图。 3种情况,然后对 3种情况的状态用点群不可约表示直积处理,最后群分解,得到 3种情况中 2个电子相互作用产生的谱项能级分裂,将这些结果画在图的右边,与弱场的左图联系起来,得到 d2离子在八面体场中的能级相关图。 |
|
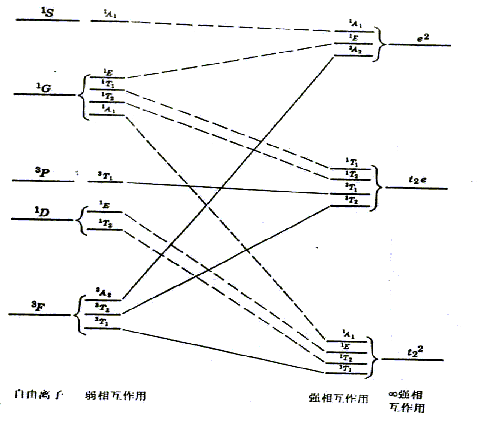
图6-15 d 2离子在八面体场中的能级相关图
|
|
对于弱配体(卤素等配体)的配合物,该图的左边可用于光谱的磁学数据的解释,对于强配体(如 CO、 CN-
等)配合物,则遵循图右边的能级分裂关系。对于介于强弱配体之间的,如 H2O、 NH3等配体形成的化合物,我们可从两种方案的连线中的某一位置,得到化合物基态与激发态的关系。
|
|
同理,我们也可得到 d3、 d4、 d5组态在八面体场中的能级相图。
|
|
(4)空穴规则:
|
|
前面曾提到: d2与 d8、 d3与 d7, d4与 d6即 dn与 d10-n对弱场体系有完全相同的能级分裂,对强场体系 d2与 d8,
|
|
|
|
t2g轨道能级较低, t2g轨道电子填得越多,能级越低,所以 d8组态的三种情况中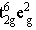 能量最低, 能量最低,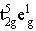 其次, 其次,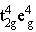 能级最高,在 d8组态中要把 能级最高,在 d8组态中要把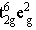 部分的能级分裂整体移到最低处, 部分的能级分裂整体移到最低处,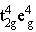 这部分放在最高,即可得到 d8组态八面体场中的能级相关图。 这部分放在最高,即可得到 d8组态八面体场中的能级相关图。
|
|
(5)更普遍的关系:
|
|
以上是讨论 dn组态在八面体场中能级相关,对四面体场( Td), d轨道分裂也是 e与 t2,只是能量颠倒过来,所以我们可以提出更普遍的关系:互为颠倒关系。
|
|
dn(八面体 )= d10-n(四面体 )与 dn(四面体 )= d10-n(八面体 )
|
|
我们只要作出下列几种相关图: d1(八面体 ), d2(八面体 ), d3(八面体 ), d4(八面体 ), d5(八面体 )就能得到 d1-d9在八面体和四面体环境中 18种可能情况的相关图。其中 d5是特殊的,它四种相关图是等同的,因为 n=5时, dn=d10-n,且 d5(八面体 )=d5(四面体 )。
|
|