|
§7.3 晶体微观结构
一.微观对称元素
周期性是晶体结构最基本的特点,我们可用空间点阵与平移来描述晶体结构,它与分子对称性不同,分子的所有对称元素必须交于一点,是一种点对称性。而晶体是要描述一种具有无穷点的空间点阵结构,除了分子对称所拥有的旋转轴、对称面、对称心等对称元素外,晶体结构还有其特有的对称元素。下面一一介绍:
1.平移——点阵:
平移是晶体结构中最基本的对称操作,可用T来表示
Tmnp=ma+nb+pc
m,n,p为任意整数
即一个平移矢量Tmnp作用在晶体三维点阵上,使点阵点在a方向平移m单位,b方向平移n单位,c方向平移p单位后,点阵结构仍能复原。
2.旋转——旋转轴:
如果晶体绕1个旋转轴转动α=2π/n角度,则称旋转轴为n重旋转轴,能够和空间点阵共存的旋转轴仅有5种,即1,2,3,4,6重旋转轴。在分子对称性中对称元素用Schoflies符号,而晶体结构中习惯用国际符号,n表示n重旋转轴,还有些图形表示方法,如表7-1所示。
晶体结构只允许存在1,2,3,4,6五种旋转轴,可证明如下:
|
设在晶体结构中取一平面点阵N1
N2 ……N7 N8……点阵点间最近间隔单位a,有一n重旋转轴位于N2,垂直于画面,顺时针方向旋转α=2π/n角度,使N1点转到N5位置,同时在N3处有另一n重旋转轴,使N4点逆时针方向转到N7位置。
|
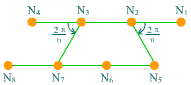
图7-15 |
|
根据点阵特点N5N7=ma
m为整数,又从三角函数关系可知:
N5N7=a+2acos2π/n
ma=a+2acos2π/n
m=1+2cos2π/n
cos2π/n最大值为1
∴|(m-1)/2|≤1
(m-1)可取值为-2,-1,0,1,2
对应的n重轴为1,2,3,4,6重轴。
|
3.反映——反映面:
若物体含有一个对称面,那么在对称面一侧的每一点,都可在对称面的另一侧找到它的对应点。另一种特殊情况是物体本身是一个平面物体,被包含在对称面内,则平面上每一点与自己对应。
4.旋转反演——反轴:
这是一个复合操作,即绕轴旋转2π/n后,再按对称中心反演后,图形仍能复原,我们称这轴为反轴,记为n。这一对称操作与分子对称性中介绍的映轴Sn是一个相关操作。相互间的联系如下:

 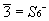
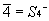
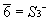
一般在分子对称点群中用映转轴,在晶体空间群中用反轴。特别指出,
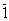 实际就是对称心,但在晶体中习惯用
实际就是对称心,但在晶体中习惯用 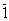 ,而不用对称心i。
,而不用对称心i。
5.螺旋旋转——螺旋轴:
复合操作由旋转加平移组成。这一对称操作与下一个对称操作反映滑移(滑移轴)都是晶体点阵对称性所特有的。我们观看跳水比赛时,可看到运动员作转身360°或720°,同时作自由落体运动。运动员所完成的动作就是螺旋旋转下降的动作。或用一螺旋、螺母固定某一部件,螺旋上紧的过程就是螺旋旋转运动。
螺旋轴用nm符号表示,即晶体点阵在螺旋轴作用下,转动2π/n角度的过程中,还沿着旋转轴平移m/n个单位。例如21螺旋轴表示:图形绕旋转轴转动180°,同时沿轴方向平移1/2个矢量单位。轴次为n的螺旋轴有(n-1)种,即选择m/n×360°时,同时平移m/n个单位,记为nm,m=1,2……,n-1。所以,4次螺旋轴,可有41、42、43三种,分别为旋转90°,平移1/4个单位;旋转180°,平移2/4个单位;旋转270°,平移3/4个单位。
6.反映滑移——滑移面:
这个动作是图形按对称面反映后,还沿着反映面的某方向平移1/n个单位,再复原。滑移面分三类:一类是反映后沿着a、b、c晶轴平移1/2个单位的,分别称a、b、c轴滑移面;一类是反映后沿着a、b轴或a、c轴或b、c轴对角线方向平移1/2个单位的,称对角滑移面,记为n;第三类是在金刚石结构中存在的滑移面,反映后沿(a+b)、(b+c)或(a+c)方向平移1/4单位,称d滑移面或金刚石滑移面。
表7-5
晶体对称元素的符号
|
对称元素
|
符号
|
图示
|
|
垂直于投影面
|
平行于投影面
|
|
旋转轴
|
2 3
|


|
|
|
|
4 6
|


|
|
|
反轴
|

|


|
|
|
|
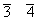
|


|
|
|
|
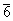
|

|
|
|
螺旋轴
|
21
|

|
|
|
|
31 32
|


|
|
|
|
41 42 43
|



|
|
|
|
61 62
|


|
|
|
|
63 64 65
|



|
|
|
反应面
|
m
|

|
 或
或 
|
|
轴滑移面
|
a b
|

|
 或
或 
|
|
c
|

|
|
对角滑移面
|
n
|

|

|
|
d滑移面
|
d
|

|

|
|