三.32个晶体学点群
晶体的理想外形和宏观观察到的对称性,称宏观对称性。由于宏观观察区分不了平移的差异,因此微观结构中一些特殊的螺旋轴、滑移面,在宏观中表现为旋转轴和对称面,即在宏观仍可以用点群来区分晶体的对称性,但由于晶体点阵平移性质的限制,旋转轴只能有1,2,3,4,6次轴,因此总共只有32个晶体学点群。
Cn:n=1,2,3,4,6 即C1,C2,C3,C4,C6;五个点群;
Cnv:C2v,C3v,C4v,C6v,四个点群;
Cnh:C1h=Cs,C2h,C3h,C4h,C6h,五个点群;
Sn:S3与C3h等同,不重复计算,只有S2=i,S4,S6,三个点群;
Dn:D2,D3,D4,D6,四个点群;
Dnh:D2h,D3h,D4h,D6h,四个点群;
Dnd:该类点群含有平分面σd,使映转轴次数要扩大一倍,故只有D2d,D3d
以上共27个点群,还有5个高阶群:T、Td、Tu、O、Oh。
32个点群有2种表示符号,一种是Schoenflies符号,即以上所用符号,还有一种是晶体学中通用的国际符号,第一个大写符号表示点阵形式,后面3个位置表示某方面的对称元素。
表7-3 国际符号中3个位置代表的方向
|
晶系
|
1
|
2
|
3
|
|
立方
|
a
|
a+b+c
|
a+b
|
|
六方
|
c
|
a
|
2a+b
|
|
四方
|
c
|
a
|
a+b
|
|
三方
|
a+b+c
|
a-b
|
――
|
|
正交
|
a
|
b
|
c
|
|
单斜
|
b
|
――
|
――
|
表7-4 32个晶体学点群
|
晶系
|
Shoenflies符号
|
国际符号
|
|
三斜
|
C1
S2
|
1
T
|
|
单斜
|
Cs
C2
C2h
|
m
2
2/m
|
|
正交
|
C2v
D2
D2h
|
m
m 2
2
2 2
m
m m
|
|
四方
|
C4
S4
C4h
C4v
D2d
D4
D4h
|
4
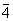
4/m
4
m m
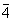 2 m
2 m
4
2 2
4/m
m m
|
|
三方
|
C3
S6
C3v
D3
D3d
|
3
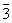
3m
3
2
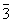 m
m
|
|
六方
|
C6
C3h
C6h
C6v
D6
D3h
D6h
|
6
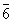
6/m
6
m m
6
2 2
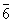 m 2
m 2
6/m
m m
|
|
立方
|
T
Th
Td
O
Oh
|
2
3
m
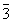
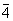 3 m
3 m
4
3 2
m
3 m
|
|