结构化学习题集
习题1:
1.1 某同步加速器,可把质子加速至具有100×109eV的动能,试问此时质子速度多大?
1.2 计算波长为600nm(红光),550nm(黄光),400nm(蓝光)和200nm(紫光)光子的能量。
1.3 在黑体辐射中,对一个电热容器加热到不同温度,从一个针孔辐射出不同波长的极大值,试从其推导Planck常数的数值:
T/℃ 1000 1500 2000 2500 3000 3500
lmax/nm 2181 1600 1240 1035 878 763
1.4 计算下列粒子的德布洛意波长
(1) 动能为100eV的电子;
(2) 动能为10eV的中子;
(3) 速度为1000m/s的氢原子.
1.5 质量0.004kg子弹以500ms-1速度运动,原子中的电子以1000ms-1速度运动,试估计它们位置的不确定度, 证明子弹有确定的运动轨道, 可用经典力学处理, 而电子运动需量子力学处理。
1.6 用测不准原理说明普通光学光栅(间隙约10-6m)观察不到10000V电压加速的电子衍射。
1.7 小球的质量为2mg,重心位置可准确到2μm,在确定小球运动速度时,讨论测不准关系有否实际意义?
1.8 判断下列算符是否是线性\厄米算符:
(1)  (2) (2)  (3)x1+x2 (4) (3)x1+x2 (4) 
1.9 下列函数是否是  的本征函数?若是,求其本征值: 的本征函数?若是,求其本征值:
(1)exp(ikx) (2)coskx (3)k (4)kx
1.10 氢原子1s态本征函数为  (a0为玻尔半径),试求1s态归一化波函数。 (a0为玻尔半径),试求1s态归一化波函数。
1.11 已知一维谐振子的本征函数为
  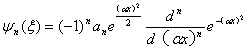
其中an和α都是常数,证明n=0与n=1时两个本征函数正交。
1.12 若  是算符 是算符  的本征函数 (B为常数), 试求α值,并求其本征值。 的本征函数 (B为常数), 试求α值,并求其本征值。
1.13 计算 Poisson 方括  , , 
1.14 证明Poisson 方括的下列性质:
(1) 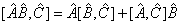
(2) 
1.15 角动量算符定义为:
 , ,  , , 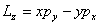
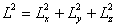
证明: (1) 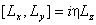 (2) (2) 
1.16 在什么条件下  ? ?
1.17 设体系处于状态  中,角动量 中,角动量  和MZ有无定值。若有其值是多少?若无,求其平均值。 和MZ有无定值。若有其值是多少?若无,求其平均值。
1.18 已知一维势箱粒子的归一化波函数为
 n=1, 2, 3 …… (其中l为势箱长度) n=1, 2, 3 …… (其中l为势箱长度)
计算 (1)粒子的能量 (2)坐标的平均值 (3)动量的平均值
1.19 试比较一维势箱粒子(波函数同上题)基态(n=1)和第一激发态(n=2)在0.4l~0.6l区间内出现的几率。
1.20 当粒子处在三维立方势箱中(a=b=c),试求能量最低的前3个能级简并度。
1.21 写出一个被束缚在半径为a的圆周上运动的质量为m的粒子的薛定锷方程,求其解。
1.22 若用一维势箱自由粒子模拟共轭多烯烃中π电子, (a)丁二烯 (b)维生素A (c)胡萝卜素分别为无色、桔黄色、红色,试解释这些化合物的颜色。
1.23 若用二维箱中粒子模型, 将蒽(C14H10)的π电子限制在长700pm, 宽400pm的长方箱中,计算基态跃迁到第一激发态的波长.
习题2:
2.1 已知氢原子的归一化波函数为 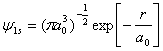
(1) 试求其基态能量和第一激发态能量。
(2)计算坐标与动量的平均值。
2.2 试求氢原子由基态跃迁到第一激发态(n=2)时光波的波长。
2.3 试证明氢原子1s轨道的径向分布函数  极大值位于 极大值位于  。 。
2.4 计算氢原子  在 在  和 和 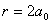 处的比值。 处的比值。
2.5 已知s和pz轨道角度分布的球谐函数分别为:  , ,  ,试证明s和pz轨道相互正交。 ,试证明s和pz轨道相互正交。
2.6 试画出类氢离子  和3dxy轨道轮廓,并指出其节面数及形状。 和3dxy轨道轮廓,并指出其节面数及形状。
2.7 原子的5个d轨道能量本来是简并的,但在外磁场的作用下,产生Zeeman效应(能量分裂),试作图描述这种现象。
2.8 试证明球谐函数Y10、Y21、Y32是方程  的本征函数。 的本征函数。
2.9 已知氢原子2pz轨道波函数为 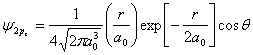
① 计算2pz轨道能量和轨道角动量;
② 计算电子离核的平均距离;
③ 径向分布函数的极值位置。
2.10已知氢原子2s 轨道波函数为

试求其归一化波函数。
2.11 类氢离子的1s轨道为:  ,试求径向函数极大值离核距离,试问He+与F6+的极大值位置。 ,试求径向函数极大值离核距离,试问He+与F6+的极大值位置。
2.12 证明类氢离子的电子离核的平均距离为 
2.13 写出Li2+离子的Schrödinger方程,说明各项的意义,并写出Li2+离子2s态的波函数
① 计算径向分布函数最大值离核距离;
② 计算1s电子离核的平均距离;
③ 比较2s与2p态能量高低。
2.14 画出4f轨道的轮廓图, 并指出节面的个数与形状.
2.15 写出Be原子的Schrödinger方程,计算其激发态2s12p1的轨道角动量与磁矩。
2.16 根据Slater规则, 说明第37个电子应填充在5s轨道,而不是4d或4f轨道.
2.17 已知N原子的电子组态为1s22s22p3
① 叙述其电子云分布特点;
② 写出N的基态光谱项与光谱支项;
③ 写出激发态2p23s1的全部光谱项。
2.18 已知C原子与O原子电子组态分别为1s22s22p2与1s22s22p4,试用推导证明两种电子组态具有相同的光谱项,但具有不同的光谱支项,简要说明原因。
2.19 写出下列原子的基态光谱项与光谱支项:Al、S、K、Ti、Mn。
2.20 写出下列原子激发态的光谱项:
C[1s22s22p13p1] Mg[1s22s22p63s13p1] Ti[1s22s22p63s23p63d34s1]
2.21 基态Ni原子可能的电子组态为[Ar]3d84s2或[Ar]3d94s1。由光谱实验测定能量最低的光谱项为3F4,试判断其属于哪种组态。
2.22 根据Slater规则,求Ca原子的第一、二电离能。
2.23 计算Ti原子第一、二电离能。
习题3
3.1 寻找下列生活用品中所含的对称元素:剪刀、眼镜、铅笔(削过与未削)、书本、方桌。
3.2 CO和CO2都是直线型分子,试写出这两个分子各自的对称元素。
3.3 分别写出顺式和反式丁二稀分子的对称元素。
3.4 指出下列几何构型所含的对称元素,并确定其所属对称点群:
(1)菱形 (2) 蝶形 (3)三棱柱 (4) 四角锥 (5) 圆柱体 (6) 五棱台
3.5 H2O属C2v点群,有4个对称元素:E、C2、  、 、  ,试写出C2v点群的乘法表。 ,试写出C2v点群的乘法表。
3.6 BF3为平面三角形分子,属D3h点群,请写出其12个对称元素,并将其分为6类。
3.7 二氯乙烯属C2h点群,有4个对称元素:E、C2、  、i,试造出C2h点群的乘法表。 、i,试造出C2h点群的乘法表。
3.8 判断下列分子所属的点群:苯、对二氯苯、间二氯苯、氯苯、萘。
3.9 指出下列分子中的对称元素及其所属点群:
SO2(V型)、P4(四面体)、PCl5(三角双锥)、S6(船型)、S8(冠状)、Cl2。
3.10 指出下列有机分子所属的对称点群:
①  ② ②  ③ ③  ④ ④  ⑤ ⑤ 
3.11 对下列各点群加入或减少某些元素可得到什么群?
① C3+i ② C3+sh ③ T+i ④ D3d-i ⑤ D4h-σh
3.12 试用对称操作的表示矩阵证明:
⑴ 
⑵ 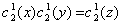
⑶ 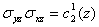
3.13 判断下列说法是否正确,并说明理由:
(1). 凡是八面体配合物一定属于Oh点群
(2). 异核双原子分子一定没有对称中心
(3). 凡是四面体构型分子一定属于Td点群
(4). 在分子点群中,对称性最低的是C1,对称性最高的是Oh群
3.14 CoCl63+是八面体构型的分子,假设两个配位为F原子取代,形成CoCl4F2分子,可能属于什么对称点群?
3.15 环丁烷具有D4h对称,当被X或Y取代后的环丁烷属什么对称点群?
①  ② ②  ③ ③  ④ ④ 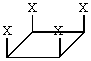
⑤  ⑥ ⑥  ⑦ ⑦  ⑧ ⑧ 
3.16 找出下列分子对称性最高的点群及其可能的子群:
① C60 ② 二茂铁(交错型) ③ 甲烷
3.17 根据偶极矩数据,推测分子立体构型及其点群:
① C3O2 (μ=0) ② H-O-O-H (μ=6.9×10-30C·m)
③ H2N-NH2 (μ=6.14×10-30C·m) ④ F2O (μ=0.9×10-30C·m)
⑤ N≡C-C≡N (μ=0)
3.18 已知连接苯环上C-Cl键矩为5.17×10-30C·m,C-CH3键矩为-1.34×10-30C·m,试推算邻位、间位、对位C6H4ClCH3的偶极矩(实验值分别为4.15×10-30、5.49×10-30、6.34×10-30C·m)
3.19 请判断下列点群有无偶极矩、旋光性:
3.20 指出下列分子所属的点群,并判断其有无偶极矩、旋光性
①  ② IF5 ② IF5
③ 环己烷(船式和椅式) ④ SO42-(四面体)
⑤  (平面) ⑥ (平面) ⑥ 
⑦ XeOF4(四方锥) ⑧ 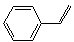
3.21 已知C6H5Cl 和C6H5NO2偶极矩分别为1.55D 和3.95D, 试计算下列化合物的偶极矩:
(1) 邻二氯苯 (2) 间二硝基苯 (3) 对硝基氯苯 (4) 间硝基氯苯 (5) 三硝基苯
3.22 已知立方烷C8H8为立方体构型,若2个H、3个H分别为Cl取代:
① 列出可形成的C8H6Cl2、C8H5Cl3可能的构型与所属的点群;
② 判别这些构型有无偶极矩、旋光性。
3.23 下列分子具有偶极矩,而不属于Cnv群的是
① H2O2 ② NH3 ③ CH2Cl2 ④H2C=CH2
3.24 下列各组分子或离子中,有极性但无旋光性是
① N3- ② I3- ③ O3
3.25 由下列分子的偶极矩数据,推测分子的立体构型及所属的点群
|
⑴CS2 |
μ=0 |
⑷N2O |
μ=0.166D |
|
⑵SO2 |
μ=1.62D |
⑸O2N-NO2 |
μ=0 |
|
⑶PCl5 |
μ=0 |
⑹H2N-NH2 |
μ=1.84D |
3.26 将分子或离子按下类条件归类:
CH3CH3,NO2+, (NH2)2CO,C60,丁三烯,B(OH)3,CH4,乳酸
⑴既有极性又有旋光性
⑵既无极性有无旋光性
⑶无极性但由旋光性
⑷有极性但无旋光性
3.27 对D6点群求出各表示的直积,并确定组成它们的不可约表示
A1×A2, A1×B1, B1×B2, E1×E2
3.28  分子属D2h点群,试写π电子组成的可约表示,并将其化成不可约表示的直和。 分子属D2h点群,试写π电子组成的可约表示,并将其化成不可约表示的直和。
|



