1.量子数的取值与上限 |
求解R方程过程中,要使拉盖尔函数成为有限多限式,必须使幂级数第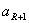 项为0。由此得到: 项为0。由此得到: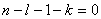
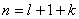 |
k是多项式中的项数,所以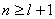 ,反之 ,反之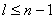 |
即Θ方程中要求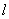 取值为0,1,2…正整值,R方程则给出 取值为0,1,2…正整值,R方程则给出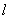 的上限为n-1。 的上限为n-1。 |
从Φ方程得出: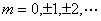 |
Θ方程给出: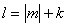 |
即给出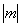 的上限 的上限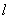 为所以 为所以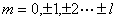 |
2.角量子数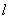 的物理意义: 的物理意义:
|
|
主量子数n决定体系的能量,接下来会进一步讨论。 |
而角量子数取值分别为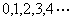 时,它所对应的原子轨道分别是 时,它所对应的原子轨道分别是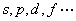 ,不仅如此,电子在绕原子 ,不仅如此,电子在绕原子 |
核作园周运动时,有一力学量——角动量,表达为算符形式是 ,参照经典力学可将 ,参照经典力学可将 |
|
其写成行列式: |
|
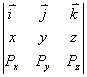 则 则
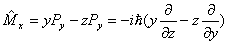
|
|
这是直角坐标形式,写成球极坐标形式: |
|
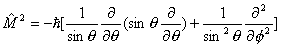
|
这形式与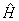 中有关变量Θ,Φ部分十分相似。实际上角动量算符平方 中有关变量Θ,Φ部分十分相似。实际上角动量算符平方 与能量算符 与能量算符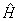 有共同本征函数 有共同本征函数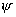 ,所以我们可写出角动量的本征方程 ,所以我们可写出角动量的本征方程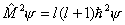 ,本征值为 ,本征值为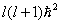 ( (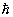 是单位).角动量不为0的电子在磁场中运动会产生磁矩 是单位).角动量不为0的电子在磁场中运动会产生磁矩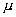 , , 的值也与角量子数有关 的值也与角量子数有关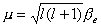 其中 其中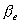 为玻尔(Bohr)磁子。 为玻尔(Bohr)磁子。 |
当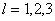 时,即 时,即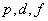 电子的磁矩分别是 电子的磁矩分别是 |
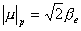  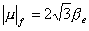 |
|
即随着量子数的增大,电子受磁场的影响越来越大 |
3.磁量子数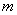
|
对一个给定的角量子数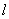 , ,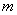 的取值为 的取值为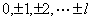 ,也就是说一个角量数 ,也就是说一个角量数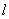 的电子,它的 的电子,它的 取值可为 取值可为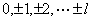 ,共 ,共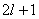 个,这就是s轨道只有一个,而p轨道有三个,d轨道有五个,f轨道有七个的原因,
s电子的轨道为球形对称分布,磁矩为0。p电子当m为0,即 个,这就是s轨道只有一个,而p轨道有三个,d轨道有五个,f轨道有七个的原因,
s电子的轨道为球形对称分布,磁矩为0。p电子当m为0,即 的磁矩与磁场方向垂直, 的磁矩与磁场方向垂直,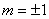 时, 时,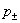 的磁矩在磁场方向分量为 的磁矩在磁场方向分量为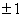 ,d电子的磁矩在磁场作用下,分裂成五个值, ,d电子的磁矩在磁场作用下,分裂成五个值,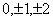 。m
的取值是电子运动产生的磁矩在z轴方向的分量,如图所示: 。m
的取值是电子运动产生的磁矩在z轴方向的分量,如图所示:
|
| 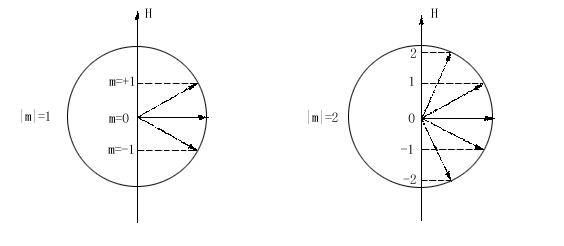
s电子轨道为球行对称分布,磁矩为0。p电子当m为0,即p0的磁矩与磁场方向垂直m=±1时,p±1的磁矩在磁场方向分量为±1 |
|
d电子的磁矩在磁场作用下,分裂成五个值0,±1,±2 |
图2-1
|