|
§2.4 原子光谱项(Atomic spectra)
一.原子光谱项定义
多电子原子,由于电子间的相互作用,原子轨道能级不再是按主量子数n分成几个简单的能级,而是与电子的角量子数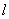 有关,与电子的自旋运动有关,分成许多更细的能级.
我们从原子光谱可观察到这种现象,化学中用原子光谱项来描述这种现象。讨论原子中电子运动耦合时有两个方法,一个是L-S耦合,一个是J-J耦合,对于轻元素,大多选择L-S耦合。 有关,与电子的自旋运动有关,分成许多更细的能级.
我们从原子光谱可观察到这种现象,化学中用原子光谱项来描述这种现象。讨论原子中电子运动耦合时有两个方法,一个是L-S耦合,一个是J-J耦合,对于轻元素,大多选择L-S耦合。 |
|
用量子数L表示电子轨道角动量的矢量加和: |
|
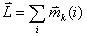
|
|
用量子数S表示电子自旋运动的矢量加和: |
|
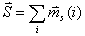
|
图2-5两个电子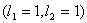 轨道角动量相互作用产生L=0,1,2的三种可能情况 轨道角动量相互作用产生L=0,1,2的三种可能情况 |

|
L值取0,1,2,3,4,5……可用大写字母S,P,D,F,G,H……表示,就象以前量子数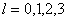 ,对应s,p,d,f轨道一样: ,对应s,p,d,f轨道一样: |
|
L
|
0 |
1 |
2 |
3 |
4 |
5 |
| 谱项 |
S |
P |
D |
F |
G |
H |
| 对应状态数 |
1 |
3 |
5 |
7 |
9 |
11 |
|
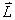 沿磁场的分量以 沿磁场的分量以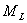 表示,其值为 表示,其值为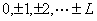 ,共(2L+1)个,即S谱项对应一个原子状态,P谱项对应三个状态,D谱项对应五个状态……将(2S+1)的数值写在L的左上角, ,共(2L+1)个,即S谱项对应一个原子状态,P谱项对应三个状态,D谱项对应五个状态……将(2S+1)的数值写在L的左上角,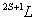 即原子光谱项,(2S+1)是 即原子光谱项,(2S+1)是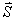 沿磁场方向的能级分裂 沿磁场方向的能级分裂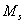 为(2S+1),M数值为 为(2S+1),M数值为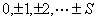 (电子偶数个,S为整数)或: (电子偶数个,S为整数)或: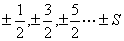 (电子数 (电子数 |
为奇数,S为半整数),(2S+1)称为光谱项的多重性。光谱项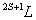 对应电子运动的(2S+1)(2L+1)个状态。 对应电子运动的(2S+1)(2L+1)个状态。 |
|
|
例如: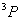 对应九个状态, 对应九个状态,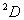 对应电子运动10个状态。 对应电子运动10个状态。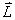 和 和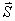 再耦合,可得到总角动量 再耦合,可得到总角动量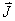 , ,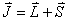 ,当 ,当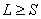 时, 时,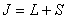 , ,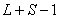 …… ……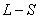 ,共(2S+1)个值,当 ,共(2S+1)个值,当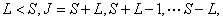 共 共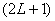 个值,写成 个值,写成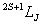 形式,称光谱支项。 形式,称光谱支项。 |
|
|
例如: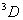 谱项(L=2,S=1)
J=3,2,1, 即 谱项(L=2,S=1)
J=3,2,1, 即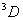 可分裂为 可分裂为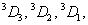 三个光谱支项。 三个光谱支项。 |
又如: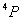 谱项 谱项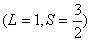 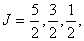 即 即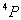 可分裂为 可分裂为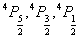 三个光谱支项。电子若处在磁场中,则J值还可分裂成(2J+1)个分量, 三个光谱支项。电子若处在磁场中,则J值还可分裂成(2J+1)个分量,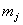 取值为 取值为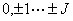 或 或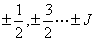 |
|