二、原子光谱项的推导
|
1.非等价电子组态 |
两个电子的主量子数或角量子数不同时,称之为非等价电子,如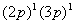 或 或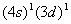 。由于至少有一个量子数不同,光谱项的推求较容易,只要将L,S耦合起来,即可求出所有可能的光谱项。例如: 。由于至少有一个量子数不同,光谱项的推求较容易,只要将L,S耦合起来,即可求出所有可能的光谱项。例如: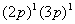 组态, 组态,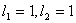 ,两矢量加和可得 ,两矢量加和可得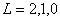 三种情况,自旋为 三种情况,自旋为 加和可得到 加和可得到 |
S=1,0,L与S不同组合都可存在,即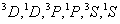 ,共六个谱项,每个谱项分别包含(2L+1)(2S+1)个微观状态,共有36个状态。另一方面,从 ,共六个谱项,每个谱项分别包含(2L+1)(2S+1)个微观状态,共有36个状态。另一方面,从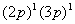 推算,2p共有三个轨道,一个电子的自旋向上或向下填入这三个轨道,共有六种可能,3p轨道填一个电子也是如此,因此有36种可能,与光谱项状态数加和结果一致。再如 推算,2p共有三个轨道,一个电子的自旋向上或向下填入这三个轨道,共有六种可能,3p轨道填一个电子也是如此,因此有36种可能,与光谱项状态数加和结果一致。再如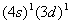 ,一个电子填在一个s轨道内可自旋向上或向下,有二种可能,而一个电子填在五个d轨道中则有十种可能,10个微观状态,二个电子的L-S耦合可得L=2,S=1,0,
则光谱项可组合出 ,一个电子填在一个s轨道内可自旋向上或向下,有二种可能,而一个电子填在五个d轨道中则有十种可能,10个微观状态,二个电子的L-S耦合可得L=2,S=1,0,
则光谱项可组合出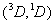 两项 两项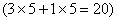 。 。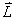 与 与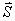 矢量再耦合,可得总角动量J,即 矢量再耦合,可得总角动量J,即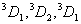 和 和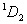 ,四个光谱支项。 ,四个光谱支项。 |
| 2.等价电子组态
|
处在同一个主量子数角量子数的电子,称之为等价电子,如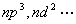 ,由于受Pauli不相容原理的限制,微观状态大大减少,光谱项推算的难度也增大。 ,由于受Pauli不相容原理的限制,微观状态大大减少,光谱项推算的难度也增大。
|
| (1)等价电子可能的微观状态
|
先讨论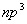 可能状态数,np的三个轨道中,电子可按自旋向上与向下两个选择填入,共有六种可能性,现有三个电子,在六种状况中选择三个,用组合 可能状态数,np的三个轨道中,电子可按自旋向上与向下两个选择填入,共有六种可能性,现有三个电子,在六种状况中选择三个,用组合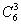 来计算, 来计算,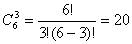 有20个微观状态,又如 有20个微观状态,又如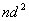 组态,nd的五个轨道,电子还有自旋的两种选择,共有十种可能性,两个电子填入这些轨道,即 组态,nd的五个轨道,电子还有自旋的两种选择,共有十种可能性,两个电子填入这些轨道,即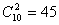 种状态,要比非等价电子的可能状态少得多。现以 种状态,要比非等价电子的可能状态少得多。现以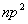 组态为例,说明如何推导等价电子的光谱项。 组态为例,说明如何推导等价电子的光谱项。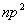 组态可能的微观状态为 组态可能的微观状态为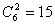 种,现具体列出如下: 种,现具体列出如下: |
表2-1 |
| |
| (2)推算原子光谱项
|
从15种可能的微观结构中,首先取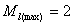 (对应的 (对应的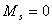 的状态),可写出光谱项 的状态),可写出光谱项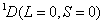 每个谱项 每个谱项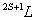 对应(2S+1)(2L+1)个微观状态,即 对应(2S+1)(2L+1)个微观状态,即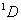 对应五个微观状态 对应五个微观状态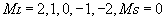 。然后再根据 。然后再根据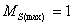 ,相对应的 ,相对应的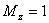 ,我们可以写出另一谱项 ,我们可以写出另一谱项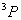 , 该谱项对应着九个微观状态 , 该谱项对应着九个微观状态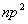 , 共有15个微观状态,其中 , 共有15个微观状态,其中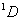 表示五个状态, 表示五个状态,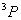 表示九个状态,最后一个状态是 表示九个状态,最后一个状态是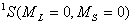 . 这样我们得到了 . 这样我们得到了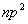 组态的全部光谱项 组态的全部光谱项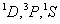 。从表2可看出,第1,15状态属 。从表2可看出,第1,15状态属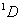 谱项。2,5,9,10,13,14状态属于 谱项。2,5,9,10,13,14状态属于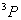 ,还有些状态,如6,7,8都是 ,还有些状态,如6,7,8都是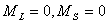 ,很难指认哪一个状态属于 ,很难指认哪一个状态属于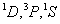 。这种情况我们可用图来表示。 。这种情况我们可用图来表示。 |
|
图2-5 np2的十五种可能状态 |
以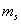 为横坐标, 为横坐标,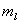 为纵坐标,首先写出的 为纵坐标,首先写出的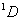 谱项,对应的 谱项,对应的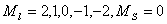 ,可在纵坐标上用五个X表示,其次 ,可在纵坐标上用五个X表示,其次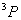 谱项 谱项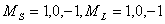 ,共九个状态用0表示,最后 ,共九个状态用0表示,最后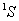 谱项 谱项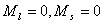 用方块表示,从图中可看出 用方块表示,从图中可看出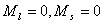 是三个状态共用一个点,我们可用这三个状态组合起来表示三个状态。 是三个状态共用一个点,我们可用这三个状态组合起来表示三个状态。 |
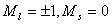 是一个点对应两个状态,也要用态迭加来处理。由于Pauli原理的限制,等价电子的 是一个点对应两个状态,也要用态迭加来处理。由于Pauli原理的限制,等价电子的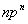 与 与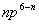 组态有相同光谱项, 组态有相同光谱项,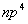 的光谱项也是 的光谱项也是 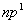 与 与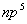 有相同的光谱项, 有相同的光谱项,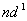 与 与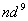 , ,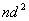 与 与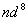 , ,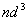 与 与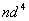 , ,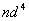 与 与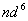 都有相同的光谱项。 都有相同的光谱项。 |
| |
|
|