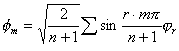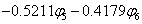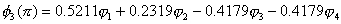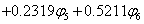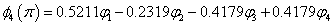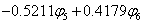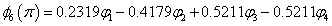|
|
|||||||||||||||||||||
|
||||||||||||||||||||||
| 当前位置 ->§ 5 多原子分子一 -> 5.4 分子轨道先定系数法
-> 5.4.1 介绍 |
|
§5.4 分子轨道先定系数法 一、介绍 本节介绍张乾二教授等提出的Hückel先定系数法。 从HMO法的论述可以看到，通常的计算是首先展开行列式，得到一个高次方程（称本征方程），并解得能量本征值。将其一一代入久期方程，求得相应分子轨道的系数。显然这种计算方法非常麻烦。虽然应用群论的方法，根据分子的对称性约化行列式方程，可以大大简化计算，但在简化计算的过程中，必须计算原子轨道的库仑积分，计算属于同一不可约表示的原子轨道的共振积分，而且要对分子分别一一计算，这些都是很冗长的。 鉴于上述的原因，应当注意到在一些共轭体系中，分子轨道的系数是分子几何构型的直接反映，并考虑到分子点群的对称性和分子排列的 "准周期 "性之间的关系，张乾二教授等提出的分子轨道图形方法叫先定系数法，它不仅把求系数和求久期方程的方法统一起来，使计算简化，而且对于同系物或结构类型相同的共轭分子能给出统一的解析表达式。现结合丁二烯，介绍如下： 丁二烯的久期方程如下：
若令
因此，对于直链多烯烃，可得到如下的一般系数（称 AO系数）图式
同时，综合 (5-4-1)和 (5-4-2)可以得到如下的循环公式：
即任一原子的 AO系数乘以 2cosθ等于邻近原子的 AO系数之和。 而参数 θ可由边界条件 Cn+1=0 得到 , 即
其中 例如丁二烯， n=4, sin5θ=0
∴ 结果与前面（ 5.3）一致。 对于己三烯， n=6, 边界条件为 sin7θ=0, 相应的能级和分子轨道为 计算结果如下表
由上面丁二烯和己三烯的分子轨道表示式我们看到，直链多烯烃分子轨道可以分为对称和反对称两种类型。若分子轨道对于二次轴为对称的，则对于对称面为反对称，若分子轨道对于对称面为对称的，那么对于二次轴就为反对称。因此，直链多烯烃体系可以按其对称性质进行分类。在此情况下，我们以偶分子和奇分子分别进行讨论。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
=
（5-4-2） 
(m=1.2.3…n)
为归一化因子
(
m=1, 2, 3, 4, 5, 6,) 
|
