|
以后相继合成出的多种系列的硼烷化合物,一类是开放式硼烷有巢状和网状,通式为BnHn+m,另一类是封闭型的硼烷,通式为BnH2-n。对巢型、网型硼烷BnHn+m,Lipscomb提出以下关系式:
|
|
|
x=m-s |
其中s为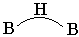 键个数 键个数 |
| t=n-s |
t为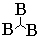 键个数
键个数 |
| y=(2s-m)/2 |
y为B-B键个数 |
|
| n为B-H端键个数,x为网中B-H键个数。 |
|
根据关系式可解出当m,n为某正整数时,有多少组(s,t,y,x)正整数解存在,即可能有多少异构体存在。
|
| 对于封闭型笼状硼烷BnH2-n,因m=0
所以s=x=0 可确定t,y即 |
|
|
|
即从定域键的观点,每个封闭型硼烷有3个B-B双中心键,n-2个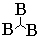 三中心键,笼的定域键个数为n+1个,端基B-H键n个,总定域键(2n+1)个,成键电子数为4n+2个,例如 三中心键,笼的定域键个数为n+1个,端基B-H键n个,总定域键(2n+1)个,成键电子数为4n+2个,例如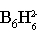 是八面体构型,笼骨架定域键为7个,B-H端键为6个,共需26个价电子成键,而 是八面体构型,笼骨架定域键为7个,B-H端键为6个,共需26个价电子成键,而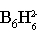 正好有26个价电子,满足要求。同样 正好有26个价电子,满足要求。同样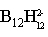 为正二十面体构型,骨架需13个定域键,端基12个氢键,共需50个价电子,而 为正二十面体构型,骨架需13个定域键,端基12个氢键,共需50个价电子,而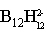 有50个价电子,可形成稳定构型,Lipscomb因此获得诺贝尔化学奖。 有50个价电子,可形成稳定构型,Lipscomb因此获得诺贝尔化学奖。
|
|
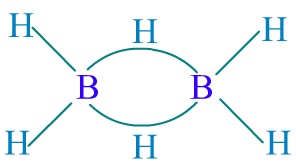
|

|
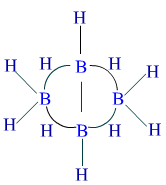
|
|
a、B2H6
|
b、B3H9
|
c、B4H10
|
|
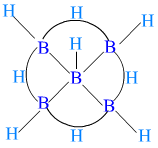
|

|
|
d、B5H9
|
e、B10H14
|
|
图6-2 常见硼烷化合物
|
|
碳硼烷化合物
|
|
巢状硼烷部分B原子被C取代,形成碳硼烷,这些碳硼烷如同环烯烃能与金属原子化合形成金属配合物如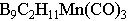 , ,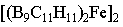 (结构如下图): (结构如下图):
|