|
(一).选择题:
1.某同学测定了三种络合物d-d跃迁光谱,但忘了贴标签,请帮他将光谱波数和络合物对应起来。
已知三种络合物为[CoF5]3-,[Co(NH3)5]3+,[Co(CN)5]3-,它们的三个光谱波数分别为34000cm-1,13000
cm-1,23000 cm-1。 (参考答案)
解:[CoF5]3-:13000
cm-1;[Co(NH3)5]3+:23000
cm-1 ;[Co(CN)5]3:34000cm-1。
2.八面体络合物中电子结构哪个将发生较大的畸变
(A)(t2g)5(eg)2 (B) (t2g)3(eg)2
(C) (t2g)4(eg)2 (D) (t2g)6(eg)3(参考答案)
3.推测下列三种络合物的d-d跃迁频率大小顺序
(1)六水合铁(III) (2) 六水合铁(II)
(3)六氟合铁(III)
(A)υ1>υ2>υ3 (B) υ1>υ3>υ2
(C) υ3>υ2>υ1 (D) υ3>υ1>υ2
(E) υ2>υ1>υ3(参考答案)
(二).计算题:
1.已知Fe(H2O) 中“2+6” 的配位场分裂能Δ0=10400
cm-1,电子成对能P=21000cm-1,Fe(CN) 中“4-6”的Δ0=33000cm-1,P=15000cm-1,试用配位场理论回答以下的问题:
(1)
比较Fe2+离子半径的大小
(2)
比较配位场稳定化能(LFSE)的大小(要具体计算)
(3)
比较磁性大小(要具体计算)(参考答案)
解:(1)Fe2+离子半径,Fe(H2O)
2+6> Fe(CN) 4+6
(2) Fe(H2O) 2+6:LFSE= -0.4Δ0 =
-4160cm-1
Fe(CN) 4+6 :LFSE= -2.4Δ0 = -79200cm-1
(3) Fe(H2O) 2+6 :μ= 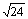 βe顺磁性
βe顺磁性
Fe(CN) 4+6 :μ=0,反磁性
2.试分别用价键理论和晶体场理论推测下列配合物的磁性,并计算其未成对电子的数目:
[Fe(CN)6]4-,[Fe(CN)6]3-,[Mn(CN)6]3-,[Fe(H2O)6]3+,[CoF5]3-(参考答案)
解:
| 配合物 |
未成对电子 |
磁性 |
| [Fe(CN)6]4- |
0 |
反磁性 |
| [Fe(CN)6]3- |
1 |
顺磁性 |
| [Mn(CN)6]3- |
1 |
顺磁性 |
| [Co(NO2)6]3- |
0 |
反磁性 |
| [Fe(H2O)6]3+ |
5 |
顺磁性 |
| [CoF5]3- |
4 |
顺磁性 |
由晶体场理论:
| 配合物 |
未成对电子 |
磁性 |
| [Fe(CN)6]4- |
0 |
反磁性 |
| [Fe(CN)6]3- |
1 |
顺磁性 |
| [Mn(CN)6]3- |
1 |
顺磁性 |
| [Co(NO2)6]3- |
0 |
反磁性 |
| [Fe(H2O)6]3+ |
5 |
顺磁性 |
| [CoF5]3- |
4 |
顺磁性 |
3.尖晶石的一般表示式为AB2O4,其中氧离子为密堆积,当金属离子A占据正四面体Td空隙时,称为正常尖晶石,而当A占据Oh空隙时,称为反尖晶石,试从晶体场稳定化能计算说明NiAl2O4晶体是什么型尖晶石结构(Ni2+为d8结构)。(参考答案)
解:假设填Td空隙
LFSE(Td)=[4×(-0.267Δ)+4×0.178Δ]=-0.356Δ
假设填Oh空隙
LFSE(Oh)=[6×(-0.4Δ)+2×0.6Δ]=-1.2Δ
因为Ni2+倾向填入稳定化能大的空隙中,所以NiAl2O4为反尖晶石
4.CoF
3-6的成对能为21000cm-1,分裂能为13000cm-1,试写出:
(1)d电子排布
(2)LFSE (3)电子自旋角动量 (4)磁矩(参考答案)
|