|
二.衍射方向
晶体衍射方向就是X射线射入周期性排列的晶体中的原子、分子,产生散射后次生X射线干涉、叠加相互加强的方向。
讨论衍射方向的方程有Laue(劳埃)方程和Bragg(布拉格)方程。前者从一维点阵出发,后者从平面点阵出发,两个方程是等效的。
1、Laue方程
(1)、直线点阵衍射的条件
设有原子组成的直线点阵,相邻两原子间的距离为α,如图7-16(α)所示,X射线入射方向S0与直线点阵的交角为α0。
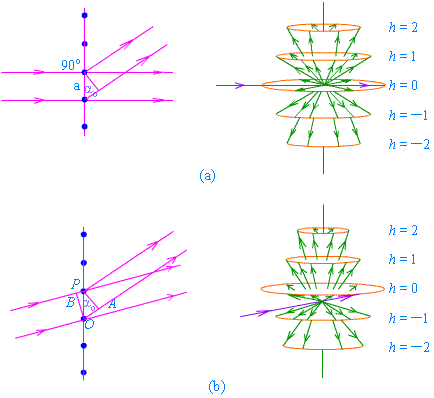
图7-16 直线点阵的衍射
若在与直线点阵交成α角的方向S1发生衍射,则相邻波列的光程差△应为波长λ的整数倍,即△=OQ-PR=hλ
h为整数。但
OQ=acosα,
PR=acosα0
故得
a(cosα-cosα0)=hλ (h=0,±1,±2,……)
这就是直线点阵产生衍射的条件。
因为由次生波原发出的X射线为球面电磁波,故与直线点阵交角为α的方向的轨迹是以直线点阵为轴的圆锥面。如上图7-16(b)所示,当α0≠90o时,h等于n和-n(n=1,2,3,…)的两套圆锥面并不对称;但当α0=90o时,h=0的圆锥面蜕化为垂直于直线点阵的平面,这时h等于n和-n的两套圆锥面就是对称的了。若放置照像板与直线点阵平行,在一般情况下所得到的是一些曲线,在α0=90o时所得到的是一组双曲线。
3、空间点阵衍射的条件
设空间点阵的三个素平移向量为a
,b和c,入射的X射线与它们的交角分别为α0,β0和γ0。衍射方向与它们的交角分别为α,β和γ,根据上述的讨论可知,衍射角α,β和γ应满足下列条件:
a(cosα-cosα0)=hλ
b(cosβ-cosβ0)=kλ
c(cosγ-cosγ0)=lλ
h,k,l,=,±1,±2,……
上式称为劳埃(laue)方程,hkl称为衍射指标。衍射指标和§3-1中所讲的晶面指标不同,晶面指标是互质的整数,衍射指标都是整数但不定是互质的。为了区别起见,在以下的讨论中我们用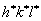 来表示晶面指标。 来表示晶面指标。
符合上式的衍射方向应是三个圆锥面的共交线。但三个圆锥面却不一定恰好有共交线,这是因为上式中的三个衍射角α,β,γ之间,还存在着一个函数关系
F(α,β,γ)=0
例如当α,β,γ相互垂直时,则有
cos2α+cos2β+cos2γ=1
α,β,γ共计三个变量,但要求它们满足上述的四个方程,这在一般情况下是办不到的,因而不能得到衍射图。为了获得衍射图必须增加一个变数。增加一个变数可采用两种办法:一种办法是晶体不动(即α0,β0,γ0固定),只让X射线;另一种办法是采用单色X射线(λ固定),但改变α0,β0,γ0的一个或两个以达到产生衍射的目的。前一种办法称为劳埃摄谱法,后一种办法包括回转晶体法和粉末法等。
2、Bragg方程
空间点阵的衍射条件除了用劳埃方程来表示以外,还有一个很简便的关系式,这就是布拉格(Bragg)方程。根据劳埃方程,我们现在要证明这样的事实,即在h=nk*、k=nk*、l=nl*的衍射中,晶面指标为(h*k*l*)的平面点阵组中的每一点阵平面都是反射面,而且其中两相邻点阵平面上的原子所衍射X射线的光程等于波长的整数倍nλ。
设X射线在入射方向的单位向量为S0,衍射方向的单位向量为S,空间点阵的三个单位平移向量为a、b和c,则劳埃方程可以写成下列的向量形式:
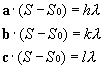
由此可得
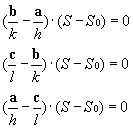
因为两个向量的数量积等于零表示两个向量互相垂直,所以从上式可知向量S—S0与向量
AB,BC,CA
垂直.这说明S-S0与△ABC所组成的平面垂直,也就是与平面点阵组(hkl)中的每一个点阵平面垂直。
如图7-19所示:

图7-17 光程差公式的推导 |
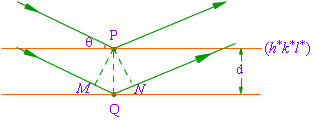
图7-18 点阵面间的反射
|
向量OP可表示为:
OP=xa+yb+zc
应用Laue方程,光程差为△=(xa+yb+zc)*(S-S0
)
= hλx
+kλy
+lλz
= nλ
我们还可以用两相邻平面点阵间的距离dhkl和衍射角θn来表示两相邻平面点阵所衍射X射线的光程差。由于这个光程差与从平面点阵中所选择的点阵点无关,所以我们可以选择两个特殊的阵点P、Q来讨论问题。如图7-20所示:
这时
△= MQ+NQ = 2d hkl sinθn
结合上面两式,则得
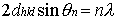
这就是布拉格(Bragg)方程。
劳埃方程和布拉格方程都是联系X射线的入射方向、衍射方向、波长和点阵常数的关系式,前者是基本的关系式,但后者在形式上更为简单,而且提供了由衍射方向计算晶胞大小的原理,故布拉格方程在X射线结构分析中有广泛的应用。
|