三.衍射强度与系统消光
以上介绍晶体衍射方向,即满足Laue方程或Bragg方程的方向将发生衍射,不满足的则不发生衍射,这是衍射的一个要素。衍射的另一个要素是衍射强度。
衍射强弱一方面与衍射方向有关(即不同的方向有不同的强度),另一方面与晶体晶胞的原子在空间的分布有关。
设晶胞中有n个原子,对衍射指标hkl的衍射方向,晶胞中每个原子对衍射强度都有自己的贡献。虽然各个原子散射的次生X射线的波长、频率、时间周期都相同,但由于衍射产生光程差导致诸波间的周相差。设第j个原子的散射因子为fj,第j个原子的散射波可用下式表示:
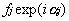 其中
其中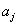 为周相差 为周相差
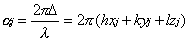
定义衍射hkl结构因子
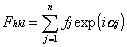
结构因子可由晶胞中各种原子的散射因子(fi)及各原子坐标参数表示
即
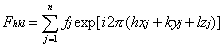
衍射hkl的衍射强度I
hkl正比于
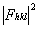 ,还与晶体对X射线的吸收、入射光强、温度等多种物理因素有关,考虑这些因素衍射强度可表示为
,还与晶体对X射线的吸收、入射光强、温度等多种物理因素有关,考虑这些因素衍射强度可表示为
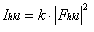
通过衍射强度数据分析,可测定晶体结构。
晶体的衍射强度有规律地、系统地为零的现象称为系统消光(systematic
absences)。系统消光的出现,是由于某些类型衍射的结构振幅数值为0,因此衍射的强度为零。系统消光是因为结构中存在螺旋轴、滑移面和带心点阵形式等晶体结构的微观对称元素所引起。通过了解晶体的系统消光现象,可以测定在晶体结构中存在的螺旋轴、滑移面和带心点阵形式。
例如晶体在c方向有二重螺旋轴(21轴),它处在晶体的坐标x=y=0处,晶胞中每一对由它联系的原子的坐标为:
x,y,z;
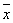 , ,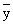 ,z+ ,z+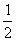
结构因子可以计算如下
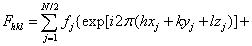 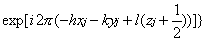
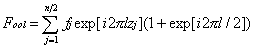
当l为偶数(即l=2n)时,
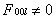
当l为奇数(即l=2n+1)时,
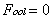
由此可见,在c方向上有二重螺旋轴时,在00l型衍射中,l为奇数的衍射强度一律为0。
面心立方晶胞原子分数坐标为:
x,y,z;x,
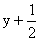 , ,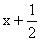 ; ;
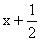 ,y, ,y,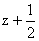 ;
;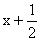 , ,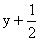 ,z。 ,z。
结构因子可表达如下:
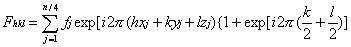
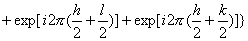
当h,k,l全为偶数或全为奇数(即h+k=2n,h+l=2n,k+l=2n)时;
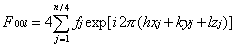
当h,k,l中有偶数又有奇数时:
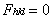
从上述结果可见,面心晶胞的衍射指标h,k,l中有偶数又有奇数存在时(如衍射指标为112,300),衍射强度一律为0。带心点阵的系统消光可从带心的倒易点阵hkl中出现的限制条件来理解。
其他螺旋轴、滑移面和带心点阵类型的系统消光的范围和性质,可用同样的原理和方法进行推引。表7.6列出晶体的带心形式和存在的滑移面、螺旋轴所出现的系统消光。
表7-6
某些晶型的系统消光和对称性
| 衍射指标类型 |
消光条件 |
消光解释 |
带心型式和对称元素记号 |
| hkl |
h+k+l=奇数
h+k=奇数
h+l=奇数
k+l=奇数
h,k,l奇偶混杂
-h+k+l不为3的倍数
|
体心点阵
C面带心点阵
B面带心点阵
A面带心点阵
面心点阵
R心点阵
|
I
C
B
A
F
R(六方晶胞)
|
| 0kl |
k=奇数
l=奇数
k+l=奇数
k+l不为4的倍数
|
(100) 滑移面,滑移量
|
b/2
c/2
(b+c)/2
(b+c)/4
|
b
c
n
d
|
| 00l |
l=奇数
l不为3的倍数
l不为4的倍数
l不为6的倍数
|
[100]螺旋轴,平移量
|
c/2
c/3
c/4
c/6
|
21,42,63
31,32,62,64
41,43
61,65
|
由表可见,当存在带心点阵时,在hkl型衍射中产生消光;存在滑移面时,在hk0,h0l,0kl等类型衍射中产生消光;而当晶体存在螺旋轴时,在h00,0k0,00l型衍射中产生消光。带心点阵的系统消光范围最大,滑移面次之,螺旋轴者最小。系统消光的范围越大,相应的对称性的存在与否就越能从系统消光现象中得到确定。
应用表7-6所列的对称性和系统消光的关系时,需要注意下面几点:
(1)要按点阵形式、滑移面和螺旋轴的顺序来了解对称性。因为一种消光规律可能包括另一种消光规律。例如,体心点阵的消光条件是h+k+l=2n+1,根据这个条件随之而来的有:在hk0型衍射中消光的有h+k=2n+1;h0l型衍射中,h+l=2n+1;在0kl型衍射中,k+l=2n+1;h00型衍射中,h=2n+1;0k0型衍射中,k=2n+1;00l型衍射中,l=2n+1等。这时并不等于在垂直于3个轴的方向上都存在n滑移面;也不等于平行于3个轴的方向都存在21,42,63螺旋轴。
(2)同一晶体可以选择多种晶胞,由系统消光所推得的晶体的微观对称性,必须和晶体中实际的晶轴取向结合起来,并表达成符合实际使用的选轴形式。
(3)消光规律一般不能给出有无螺旋轴、镜面和对称中心的判据。对称中心的有无可通过倍频效应、压电效应、旋光性及结构振幅的统计规律来判别。
|