此外，晶格的畸变（不均匀应变、微观应变、内应力）也能导致衍射线发生角位移而影响衍射峰的峰宽。设晶格畸变导致的晶面间距变化为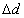
，其晶格畸变量表示为
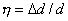，则由该晶格畸变引起的衍射线角度位移由Bragg方程决定：
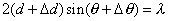或 
考虑到
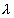和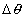
的值都很小，上式可展开并整理为
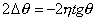或写为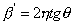 
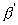为晶格畸变引起的衍射峰的宽化。
可以看出，晶粒细化和晶格畸变均能引起衍射峰的宽化；不过，这两类宽化的性质是不同的。晶粒细化引起的宽化是由于X射线的非Bragg角入射和衍射引起的，而晶格畸变引起的宽化是由于晶面间距的变化引起的衍射角的位移所致。这样，衍射峰的宽化为晶粒细化引起的宽化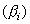
和点阵畸变引起的衍射峰宽化
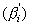的总和：
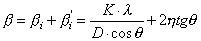
或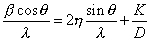
通过测量二个以上的衍射峰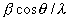，以
为y轴，以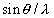
为x轴作图，所得直线的斜率为点阵畸变量
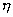的两倍，y轴上的截距为晶粒尺寸D的倒数。
实际应用中，需要根据具体情况考虑是否存在晶格畸变引起的衍射峰宽化。一般认为，氧化物等无机物相晶格畸变小，可以不考虑晶格畸变；而金属材料中（如金属电沉积层），晶体含有镶嵌块结构，由不平行的小晶块拼成的，小晶块往往会有微观畸变，此时则需考虑晶格畸变。
5. X射线衍射峰的形状（线形）――晶粒大小分布
晶粒细化会引起X射线衍射峰加宽，不同的晶粒大小导致不同的衍射峰峰宽。因此，在晶格畸变可以忽略的情况下，衍射峰的形状隐藏者晶粒大小分布的信息。粉末对X射线衍射的衍射峰线形函数为不同大小的晶粒衍射线的叠加：
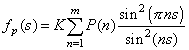
式中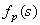
为衍射峰的线形函数，K为与平均晶胞个数相关的常数，s为倒易点阵（空间）坐标，P(n)为周期数为n的晶粒所占的比例，或称之为晶粒分布函数。
把实验样品的真实衍射峰线形(f(s)) 与衍射峰的线形函数进行拟合，就可以获得晶粒分布函数，晶粒大小分布。
6. 卫星峰――多层膜与超晶格
当由A和B两物相薄层（1纳米－10纳米）形成交替的AB/AB/AB…薄膜时，X射线衍射峰并不是宽化的A和B两物相衍射峰。多层膜的衍射峰相当复杂，随着多层膜中AB重复单层厚度的变化而变化；但总体特征为若干主峰伴随若干卫星峰，当单层厚度较大时，主峰出现在A和B的体相衍射峰附近。
实际上，多层膜的衍射可以考虑为ABABAB…超晶格的衍射，即考虑周期为AB重复单层厚度
的晶体的衍射。根据Bragg方程，则有
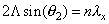
这样，在一定的X光波长的条件下，衍射峰的位置则由重复单层厚度决定的。由于
值较大，因此除了在高角度可以观察到衍射峰外，在小角度会有衍射峰。多层膜中重复单层厚度可以方便地从Bragg方程导出：
其中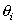
和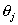
为超晶格i和j级衍射峰的位置。多层膜的高角度衍射峰中的主峰和相邻的卫星峰的衍射级数一般相差为1，卫星峰一般标为±1，±2…；因此，多层膜中重复单层厚度可以方便地从卫星峰的位置求算出来。
上面列举了X射线衍射峰包含的若干个重要的信息，此外，晶体衍射的Debye环的不均匀度与样品的择优取向（织构）有关，小角散射峰包含样品颗粒度的信息等等。
。从衍射线强度可以计算结构振幅
的值，因此，指标化成为测定结构的关键步骤。指标化就是将各条衍射线的hkl标出。对于单晶衍射，通过至少4个不共面的衍射线就可对衍射线指标化。对于多晶的衍射，衍射数据的指标化要复杂一些。但对晶胞不大的立方、四方、六方和三方晶系的晶体，多晶衍射线的指标化一般不难；其它低级晶系要难一些，若参考同晶晶体的晶胞参数，也不难指标化。
与
成正比。对于简单点阵P，没有消光规律，hkl可以是任意整数，它可采取100，110，111，200，210，211，220，221，222，300，…等数值。
，
为奇数时消光，衍射线强度为0，观测不到衍射线，即100，111，210，221，300等衍射线不出现。对于面心点阵F，hkl奇偶混杂时不出现衍射线，即100，210，211，221，300等衍射线不出现。
从低角度到高角度的衍射线的
值按下列比例分布：
射线（波长
）通过多晶X射线衍射仪测得的衍射线的角度
为：2。
可以得出，当
最小）；因此，要获得高精度的点阵参数，应尽可能多地测定高角度的衍射线。
晶粒的平均尺寸（准确的说是垂直于hkl晶面方向的晶粒的平均尺寸）
所采用的X射线的波长
由晶粒大小引起的衍射峰的宽化值（单位为弧度）
衍射峰的角度
为常数，
采用半高宽时K＝0.9，
时，衍射峰宽度与晶粒尺寸没有明显的数学关系式，而当晶粒尺寸小于1nm时，晶体已经向无定形相过渡，因此，Scherrer方程的适用范围是晶粒介于1nm至100纳米的范围。
石英经850°C退火）测得的峰宽为仪器宽化（B0）。
