|
第八章 金属与合金结构
Chapter 8. Metals and alloys
§8.1 金属键理论(The metallic bond theory)
在一百多种化学元素中，金属元素约占80% 。它们都具有金属光泽、有很好的传热导电性，金属的这些性质是它们内部结构的反映。金属元素很多，大致可分为两大类，一类为简单金属，一类为过渡金属，稀土和锕系金属。
简单金属主要指碱金属、碱土金属和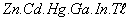 
等。在这类金属中，元素的电负性较小，电离能也较小，最外层价电子容易脱离原子核的束缚，在金属中运动。这样原子实和价电子可截然分开。前者原子实对金属整体来说，它的影响是局域的，而后者—价电子则是整体公有的。这类金属用近自由电子模型，获得了与实验大致相符的结果。贵金属
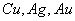介于之间，它们部分性能和简单金属相似，而另一部分性质与过渡金属相似。
另一类金属包括d壳层未填满的过渡金属、4f壳层未填满的稀土金属，5f壳层未填满的锕系金属，这些未填满的次层电子能级和外层S,P电子相近，这些d电子或f电子介于公有化与局域化状态之间，所以要有特殊的理论处理。
一.自由电子模型
简单金属的自由电子模型是个很简单的模型，价电子完全公有，构成金属中导电的自由电子，原子实与价电子间的相互作用完全忽略，自由电子之间也是毫无相互作用的理想气体。为了保持金属电中性，可设想原子实带正电分布于整个体积中，和自由电子的负电荷正好中和。
自由电子波函数可用一平面波表示
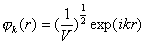其中 
为波矢量，V为金属体积，与边长L关系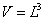 
这样自由电子类似势箱中和自由粒子，自由电子在金属中的零势场中运动
相应能量可表示为
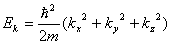
在绝对零度时，自由电子体系处于基态，N个电子占据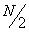 
个最低能级，最高占据能为费米能级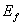 
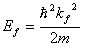
自由电子气模型完全忽略电子间的相互作用，也忽略了原子实形成的周期势场对自由电子的作用，处理结果当然与真实金属有差距，后来发展了“近自由电子模型”（即在自由电子气中引入周期势场微扰），在一定程度上反映了简单金属的实际情况，可作为金属电子结构的一级近似。近年，有人提出用赝势理论处理简单金属，即采用微弱的赝势代替电子与正离子间的相互作用势，使问题得到简化。赝势可用正交平面波法解析导出，也可用参数直接构筑模型势。例如一模型赝势为
 
 
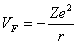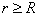
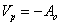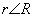即原子实半径R 以外和真实库仑势相同，在原子实范围内用一个恒值势来代替
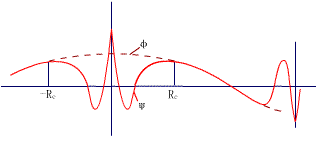
图8-1 在近自由电子模型中的电子真实波函数（实线）
和赝势波函数（虚线）
R为原子实半径。 |
