| 1.半径为R的圆球堆积成正八面体空隙,计算空隙中心到顶点的距离。
|
| 解:正八面体空隙由6个等径圆球密堆积而成,其顶点即圆球的球心,其棱长即圆球的直径。空隙的实际体积小于八面体体积。
|
| 八面体空隙中心到顶点
的距离为:
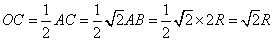
而八面体空隙中心到球面的最短距离为
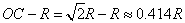
此即半径为R的等径圆球最密堆积形成的正八面体空隙所能容纳的小球的最大半径0.414是典型的二元离子晶体中正离子的配位多面体为正八面体时
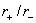 的下限值。
的下限值。
| 2.金属钠为体心立方结构,a=429pm,计算: |
| (a)钠的原子半径;(b)金属钠的理论密度;(c)
(110) 面的间距。 |
| 解:
(a)金属钠为体心立方结构,原子在晶胞对角线方向上互相接触,由此推得原子半径r和晶胞参数a的关系为:
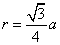
代入数据得:
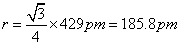 |
|
(b)每个晶胞中含两个钠原子,因此,金属钠的理论密度为:
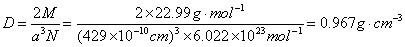
|
|
(c)
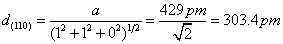
|
|
3.有一黄铜合金含Cu,Zn的质量分数依次为75%,25%,晶体的密度为8.5g·cm-3。晶体属立方面心点阵结构,晶胞中含4个原子。Cu的相对原子质量为63.5,Zn的相对原子质量为65.4。
(a)求算Cu和Zn所占的质量是多少克?
(b)每个晶胞中含合金的质量是多少克? |
(c)晶胞体积多大?
(d)统计原子的原子半径是多大? |
| 解:
(a)设合金中Cu的原子分数(即摩尔分数)为x, 则Zn的原子分数(即摩尔分数)为1-x,由题意知,63.5x:65.4(1-x)=0.75:0.25
解之得:
x=0.755, 1-x=0.245
所以,该黄铜合金中,Cu和Zn的摩尔分数分别为75.5%和24.5% |
| (b)每个晶胞中含合金的质量是:
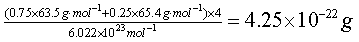
|
| (c)晶胞的体积等于晶胞中所含合金的质量除以合金的密度,即:
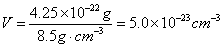
|
| (d)由晶胞的体积可以求出晶胞参数:
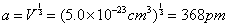
由于该合金属立方面心点阵结构,因而统计原子在晶胞面对角线方向上相互接触,由此可推得原子半径为:
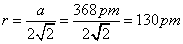
|