|
§1.2 量子力学的基本假设
(The basic assumptions in quantum mechanics)
量子力学的基本假设,象几何学中的公理一样,是不能被证明的。公元前三百年欧几里德按照公理方法写出《几何原本》一书,奠定了几何学的基础。二十世纪二十年代,狄拉克,海森伯,薛定锷等在量子力学假设的基础上构建了这个量子力学大厦。假设虽然不能直接证明,但也不是凭科学家主观想象出来的,它来源于实验,并不断被实验所证实。
假设Ⅰ——状态波函数与几率
假设Ⅱ——力学量与算符
假设Ⅲ——薛定谔方程
假设Ⅳ——态叠加原理
假设Ⅴ——Pauli不相容原理
一、状态波函数和几率
微观体系的任何状态都可用一状态波函数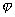 来表示。由于微观粒子无确定的外形无确定的运动轨迹,都具有波粒二象性。为了描述它们的运动状态和在空间出现的几率可能性,而选择状态波函数 来表示。由于微观粒子无确定的外形无确定的运动轨迹,都具有波粒二象性。为了描述它们的运动状态和在空间出现的几率可能性,而选择状态波函数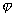 来表示。 来表示。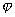 是体系包含的所有微粒的坐标 是体系包含的所有微粒的坐标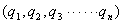 和时间 和时间 的函数,即状态函数随坐标与时间两个变量变化: 的函数,即状态函数随坐标与时间两个变量变化:
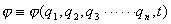
对处于三维直角坐标空间的粒子,状态波函数表示为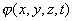 ,而在球坐标空间表示为 ,而在球坐标空间表示为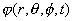
(1)为使状态波函数有确定的物理意义,数学上要求波函数满足单值,连续,平方可积三个条件:
A.单值条件:波函数与其复共轭的乘积表示该微观体系在空间的几率分布,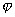 必须是单值函数,否则粒子在空间出现将出现不确定性。 必须是单值函数,否则粒子在空间出现将出现不确定性。
B.连续性:状态波函数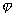 在坐标变化的全部范围内必须是连续的,因薛定谔方程是二阶微分方程,若函数不连续,就无法得到二阶微商。 在坐标变化的全部范围内必须是连续的,因薛定谔方程是二阶微分方程,若函数不连续,就无法得到二阶微商。
C.平方可积:在量子力学中要得到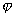 力学量的平均值,需对波函数进行积分。 力学量的平均值,需对波函数进行积分。
(2)几率与几率密度
状态波函数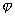 与它的复共轭的乘积 与它的复共轭的乘积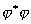 是一个几率分布函数,称几率密度。 是一个几率分布函数,称几率密度。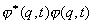 表示一个坐标为 表示一个坐标为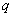 的粒子在 的粒子在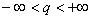 范围内运动的几率分布函数。 范围内运动的几率分布函数。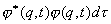 表示:处在 表示:处在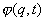 状态的粒子在 状态的粒子在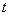 时刻,在小体积元 时刻,在小体积元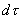 附近出现的几率。每个体系或每个粒子在整个空间出现的几率之和必须等于一。满足归一化条件,即: 附近出现的几率。每个体系或每个粒子在整个空间出现的几率之和必须等于一。满足归一化条件,即:
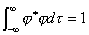
(3)描述化学体系中的微观粒子─电子的状态波函数,就是我们在化学中熟悉的原子轨道,分子轨道。
众所周知,C原子的1s,2s,2p轨道,是描述C原子中电子处在不同能级状态的波函数。C原子的2s状数态波函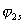 有它对应的数学函数形式, 有它对应的数学函数形式,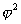 描述它的电子云在空间的分布情况。在《结构化学》中,我们只讨论与时间无关的状态,或在某一时刻的状态,也称之为定态。这时状态波函数只与坐标有关。三维空间里N个粒子体系的状态波函数为: 描述它的电子云在空间的分布情况。在《结构化学》中,我们只讨论与时间无关的状态,或在某一时刻的状态,也称之为定态。这时状态波函数只与坐标有关。三维空间里N个粒子体系的状态波函数为:
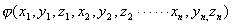
(4)波函数的正交归一性
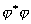 的物理意义为粒子在空间出现几率密度,所以必须满足归一化的条件,以H原子1s函数为例说明 的物理意义为粒子在空间出现几率密度,所以必须满足归一化的条件,以H原子1s函数为例说明
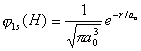
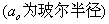
| 对1s电子和几率密度在整个空间积分: |
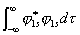 |
| 直角坐标系中,微体积元: |
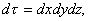 |
| 球极坐标中: |
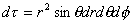 |
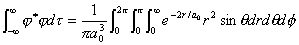
说明H原子的1s电子在整个实空间出现的几率和为1。
若两个状态波函数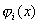 与 与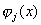 对整个空间取积分等于0: 对整个空间取积分等于0:
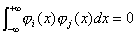
称这两个函数是相互正交的。
H原子在不同状态的波函数,如1s与2s,2s与2p等是相互正交的
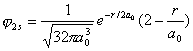
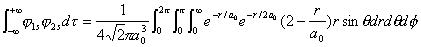
|