|
例题与习题
一、练习题
1.立方势箱中的粒子,具有
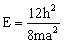 的状态量子数, 的状态量子数, 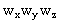 是 是
| |
A. 211 |
B. 231 |
C. 222 |
D. 213。 |
(参考答案)
2.处于状态
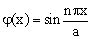 的一维势箱中的粒子,出现在 的一维势箱中的粒子,出现在 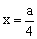 处的概率是多少? 处的概率是多少?
| |
A.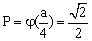 |
B.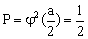 |
C.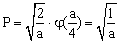 |
D.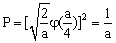 |
| |
E. 题目提法不妥,以上四个答案都不对。 |
(参考答案)
3.计算能量为100eV光子、自由电子、质量为300g小球的波长。
( 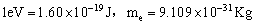 ) )
(参考答案)
4.根据测不准关系说明束缚在0到a范围内活动的一维势箱中粒子的零点能效应。(参考答案)
解: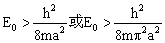 。 。
5.链状共轭分子 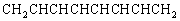 在波长方向460nm处出现第一个强吸收峰,试按一维势箱模型估计该分子的长度。(参考答案) 在波长方向460nm处出现第一个强吸收峰,试按一维势箱模型估计该分子的长度。(参考答案)
解: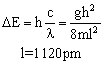
6.设体系处于状态 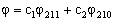 中,角动量 中,角动量 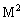 和 和 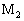 有无定值。其值是多少?若无,求其平均值。 有无定值。其值是多少?若无,求其平均值。
(参考答案)
解:角动量
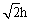 角动量平均值 角动量平均值 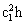
7.函数  是不是一维势箱中粒子的一种可能的状态?如果是,其能量有没有确定值?如有,其值是多少?如果没有确定值,其平均值是多少?
(参考答案) 是不是一维势箱中粒子的一种可能的状态?如果是,其能量有没有确定值?如有,其值是多少?如果没有确定值,其平均值是多少?
(参考答案)
解:可能存在状态,能量没有确定值,
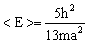
8.求下列体系基态的多重性。(2s+1) (1)二维方势箱中的9个电子。(2)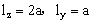 二维势箱中的10个电子。(3)三维方势箱中的11个电子。(参考答案) 二维势箱中的10个电子。(3)三维方势箱中的11个电子。(参考答案)
9.在0-a间运动的一维势箱中粒子,证明它在
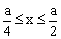 区域内出现的几率 区域内出现的几率 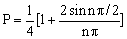 。当 。当  ,几率P怎样变? (参考答案) ,几率P怎样变? (参考答案)
解: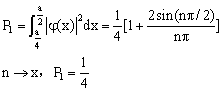
10.在长度l的一维势箱中运动的粒子,处于量子数n的状态。求
(1)在箱的左端1/4区域内找到粒子的几率?(2)n为何值,上述的几率最大?(3)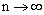 ,此几率的极限是多少?(4)(3)中说明什么?(参考答案) ,此几率的极限是多少?(4)(3)中说明什么?(参考答案)
解: 
11.一含K个碳原子的直链共轭烯烃,相邻两碳原子的距离为a,其中大π键上的电子可视为位于两端碳原子间的一维箱中运动。取l=(K-1)a,若处于基组态中一个π电子跃迁到高能级,求伴随这一跃迁所吸收到光子的最长波长是多少?(参考答案)
解: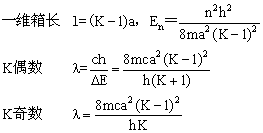
12.写出一个被束缚在半径为a的圆周上运动的质量为m的粒子的薛定锷方程,求其解。(参考答案)
解: 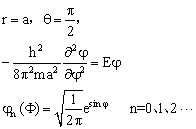
13.在什么条件下
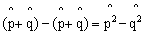 ?(参考答案) ?(参考答案)
解: 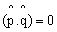
14.已知一维运动的薛定锷方程为: 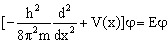 。 。 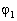 和 和 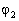 是属于同一本征值得本征函数,证明 是属于同一本征值得本征函数,证明 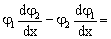 常数。(参考答案) 常数。(参考答案)
解: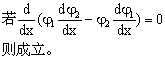
15.对立方箱中的粒子,考虑 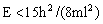 的能量范围。(1)在此范围有多少个态?(2)在此范围有多少个能级?(参考答案) 的能量范围。(1)在此范围有多少个态?(2)在此范围有多少个能级?(参考答案)
|