四、态迭加原理
若 为某一微观体系的可能状态,由它们线性组合所得的 为某一微观体系的可能状态,由它们线性组合所得的 也是该体系可能存在的状态。 也是该体系可能存在的状态。

例如,C原子中的电子可能处于2s,2p状态,也可能处于s,p组合起来的状态。当4个H原子靠近C原子要组成 分子时,为了有效成键,2s与2p轨道可进行线性组合,得到 分子时,为了有效成键,2s与2p轨道可进行线性组合,得到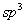 杂化轨道即线性组合后的状态,也是电子可能处于的状态。同类的例子如 杂化轨道即线性组合后的状态,也是电子可能处于的状态。同类的例子如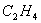 中的C原子2s,2p轨道也可组合成 中的C原子2s,2p轨道也可组合成 轨道…… 组合系数 轨道…… 组合系数 的大小,反映了在 的大小,反映了在 中各个 中各个 的贡献, 的贡献,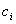 越大, 越大, 在 在 中的贡献越大。 中的贡献越大。
态迭加原理是微观世界的独特现象,与经典物理无法类比。它告诉我们体系的状态函数不是唯一的。一组原子轨道或分子轨道,经过态的迭加,可用另外一种形式来表示,例如求解类氢离子的 方程可得复数形式的p轨道(它包含3个分量 方程可得复数形式的p轨道(它包含3个分量 ),要在实空间表示它们,需对它们进行迭加: ),要在实空间表示它们,需对它们进行迭加:
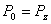


p轨道的实表示与复表示是完全等价的,对d轨道也有类似情况。
推论1:本征态力学量的平均值
设力学量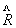 的一套本征函数为 的一套本征函数为 ,它们所对应的本征值分别为 ,它们所对应的本征值分别为 ,当体系处于本征态 ,当体系处于本征态 (且 (且 已被归一化后): 已被归一化后):

|