|
§1.3 量子力学的简单应用
(Simple applications of quantum mechanics)
一、一维势箱中的粒子
为了说明量子力学处理问题的方法、步骤,现以一维势箱中的自由粒子为例,说明如何求解它的薛定锷方程,从而获得状态本征函数与能量值。
1.薛定谔方程
有一个一维势箱如图所示,势箱长度为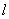 ,箱内势能 ,箱内势能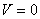 ,箱外势能为无穷大。粒子可在箱中自由运动,坐标变化范围为: ,箱外势能为无穷大。粒子可在箱中自由运动,坐标变化范围为: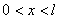
| 整理后得: |
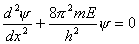 |
| 这是二阶常系数微分方程:
|
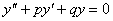 |
| 特征方程: |
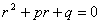
|
当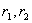 为实根时, 为实根时, |
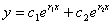
|
当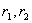 为复根时, 为复根时,
|
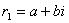
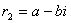 |
| 方程的通解为: |
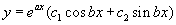
|
| 现方程的根: |
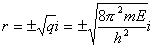
|
| 波函数通解为: |
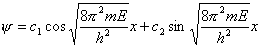 |
据边界条件,当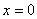 和 和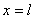 时, 时,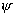 应为0 应为0
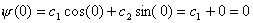 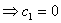
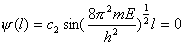
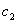 不能再为0(否则就没有波函数了) 不能再为0(否则就没有波函数了)
只能 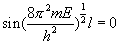 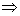
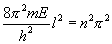
| 由此可得能量数值: |
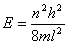
|
再将E的数值代回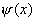 |
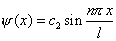 |
然后用归一法定出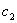
|
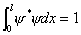
|
令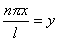
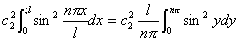
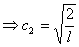

2.体系的波函数与能量
据此,我们可绘出状态波函数与几率密度函数的示意图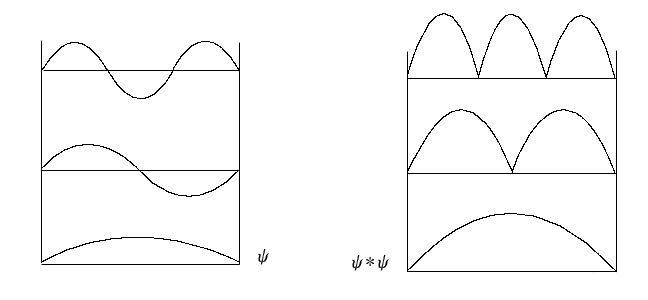
图1-6 一维势箱内自由粒子的波函数(左)和几率分布函数(右)
讨论:势箱中自由粒子的波函数是正弦函数,基态时,长度 势箱中只包含正弦函数半个周期,随着能级升高,第一激发态包含一个周期,第二激发态包含正弦波一个半周期……。随着能级升高,波函数的节点越来越多。而几率分布函数告诉我们自由粒子在势箱中出现的几率大小。例如基态时,粒子在 势箱中只包含正弦函数半个周期,随着能级升高,第一激发态包含一个周期,第二激发态包含正弦波一个半周期……。随着能级升高,波函数的节点越来越多。而几率分布函数告诉我们自由粒子在势箱中出现的几率大小。例如基态时,粒子在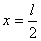 处出现几率最大。而第一激发态,粒子在 处出现几率最大。而第一激发态,粒子在 处出现几率为0。在 处出现几率为0。在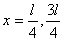 处出现几率最大。 处出现几率最大。
3.小结
从一维势箱中自由粒子的实例可看出量子力学处理微观体系的一般步骤:
(1)首先写出薛定谔方程的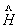 : :
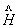 由动能与势能部分组成。N个粒子的动能通式为 由动能与势能部分组成。N个粒子的动能通式为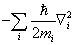 ,势能根据不同情况而异。 ,势能根据不同情况而异。
(2)简单体系的薛定谔方程为二阶线性微分方程,可先解出通解。
(3)根据边界条件定出通解中的待定系数,并用边界条件求解能量本征值。
(4)能量代回特解,并用归一化得到状态波函数。
(5)根据状态波函数和能量讨论体系的稳定性,几率分布,能级高低。
|