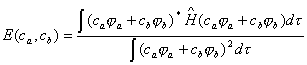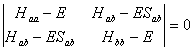变分法是解方程的一种近似方法，它基于下面的原理：对任一个品优函数，用体系的算符求得的能量平均值，将大于或接近于体系基态的能量(E₀)，即

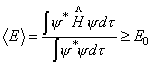
据此原理，利用求极值的方法调节参数，找出能量最低时对应的波函数，即为和体系相近似的波函数。上式可证明如下：

设 …组成一正交、归一完全的函数组，其能量依次增加，E₀≤E₁≤E₂…,由此可得

将上式中的 按照体系 的本征函数 展开

利用 的正交归一性，可得平均能量

因 恒为正值， (据1.2假设IV)，0< ≤1，

故得

所以   <E>≥E₀

常用的线性变分法是选择一品优的线性变分函数

求出E值最低时对应的c₁值。

因为电子运动到核A附近区域时，分子轨道 很像 原子轨道 ； 同样，当电子运动到核B附近区域时，分子轨道近似于 。根据态叠加原理，分子轨道可用原子轨道的线性组合表示

作为H ₂⁺ 的变分函数，式中c_a和c_b为待定参数，而

将 代入 中，得

由于H ₂⁺的两面个核是等同的，而 和 又都是归一化函数，展开

上式并令

得     

对c_a和c_b偏微商求极值，得

消去Z，因为 得

，

将Y，Z值代入，并化简 ，可得久期方程

      （4-2-2-1式）

为了使c_a和c_b有不完全为零的解，可得久期行列式

解此行列式，得E的两个解

将E1值代回（4-2-2-1式）的E，得c_a=c_b，相应的波函数

将E₂值代回（4-2-2-1式）的E，得c_a=-c_b，相应的波函数

通过波函数归一化条件，可求得