三、同核双原子分子
1.电子组态:
将体系中电子按Pauli规则填充在轨道中,分子轨道按能量顺序排列,我们可得到体系的电子组态。
H2由两个氢原子的1s轨道组合成两个分子轨道 ,
, ,两个电子填充在 ,两个电子填充在 上,H2的电子组态记为
上,H2的电子组态记为
He2有4个电子,电子组态为  ,由于成键与反键轨道都填满,成键作用与反键作用相互抵消,所以它们基本上属于原来的原子轨道。
,由于成键与反键轨道都填满,成键作用与反键作用相互抵消,所以它们基本上属于原来的原子轨道。
Li2、B2等分子的电子组态如表4—1所示
| 表4-1
同核双原子分子和离子的电子组态 |
| 分子
(离子) |
电子数 |
电子组态 |
键级 |
光谱项 |
键长
(pm) |
键解离能
(KJ·mol-1) |
| H2+ |
1 |
(σ1s)1 |
0.5 |
2Σg+ |
106 |
255.48 |
| H2 |
2 |
(σ1s)2 |
1 |
1Σg+ |
74.12 |
431.96 |
| He2+ |
3 |
(σ1s)2
(σ1s*)1 |
0.5 |
2Σu+ |
108.0 |
322.2 |
| Li2 |
6 |
KK(1σ)2 |
1 |
1Σg+ |
267.2 |
110.0 |
| B2 |
10 |
KK(1σ)2
(1σ*)2 (1π*)2 |
1 |
(3Σg—)b |
158.9 |
274.1 |
| C2 |
12 |
KK(1σ)2
(1σ*)2 (1π*)4 |
2 |
1Σg+ |
124.25 |
602 |
| N2+ |
13 |
KK(1σ)2
(1σ*)2 (1π*)4 (2σ)1 |
2.5 |
2Σg+ |
111.6 |
842.15 |
| N2 |
14 |
KK(1σ)2
(1σ*)2 (1π*)4 (2σ)2 |
3 |
1Σg+ |
109.76 |
941.69 |
| O2+ |
15 |
KK(σ2s)2
(σ2s*)2 (σ2p)2
(π2p)4 (π2p*)1 |
2.5 |
2Πg |
112.27 |
626 |
| O2 |
16 |
KK(σ2s)2
(σ2s*)2 (σ2p)2
(π2p)4 (π2p*)2 |
2 |
3Σg— |
120.74 |
493.54 |
| F2 |
18 |
KK(σ2s)2
(σ2s*)2(σ2p)2
(π2p)4(π2p*)4 |
1 |
1Σg+ |
141.7 |
155 |
从B2、C2分子可看出,由于2s、2p轨道能级的靠近,使 与
与 轨道发生混杂, 轨道发生混杂, 与
与 能量降低, 能量降低, ,
, 轨道能量升高, 轨道能量升高, 轨道被推到
轨道被推到 上面,即能量顺序为 上面,即能量顺序为

到了O2、F2分子,2s 与2p能级相差较远, 轨道能量又回到原来位置
轨道能量又回到原来位置
2.键级:
分子键级定义为成键电子数与反键电子数的差除以2。表4-1也列出了双原子分子的键级,从B2至N2分子键级逐次增多,实验测定键长逐步缩短,解离能逐步增大。从N2至F2,键级逐次降低,实验测得键长逐步拉长,解离能逐步减少,理论分析与实验完全符合。
3.分子光谱项:
双原子分子光谱项用符号 表示。 表示。
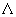 为大写希腊字母,对应分子的总轨道角动量的值。2s+1是自旋多重度,类似原子光谱项。一个分子的电子组态,如果所有的轨道是全满或全空,叫做满壳层结构,总轨道角动量为0,总自旋角动量也为0,这种结构呈 为大写希腊字母,对应分子的总轨道角动量的值。2s+1是自旋多重度,类似原子光谱项。一个分子的电子组态,如果所有的轨道是全满或全空,叫做满壳层结构,总轨道角动量为0,总自旋角动量也为0,这种结构呈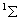 态。H2、Li2、C2、N2等基态光谱项均为 态。H2、Li2、C2、N2等基态光谱项均为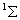 。对同核双原子分子,状态对于反演动作的对称性,可根据公式 。对同核双原子分子,状态对于反演动作的对称性,可根据公式
g×g=u×u=g,u×g=u
由各个电子的对称性相乘得出来。只有在反对称轨道上有奇数个电子时,才有u状态,
对于二重简并的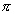 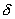 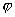 等轨道,它们的 等轨道,它们的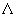 值分别对应±1,±2,±3。例如B2分子,两个电子分别占据 值分别对应±1,±2,±3。例如B2分子,两个电子分别占据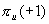 和 和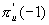 轨道,总轨道角动量的和仍为0,电子自旋角动量为1,则多重度为3,其基态光谱项为 轨道,总轨道角动量的和仍为0,电子自旋角动量为1,则多重度为3,其基态光谱项为 自旋三重态则意味着该分子是顺磁性的,两个电子亦可分别占据 自旋三重态则意味着该分子是顺磁性的,两个电子亦可分别占据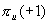 和 和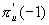 ,自旋相反,则光谱项为 ,自旋相反,则光谱项为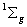 两个电子亦可占据同一个 两个电子亦可占据同一个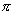 轨道,则 轨道,则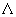 =2,自旋角动量为0,光谱项为 =2,自旋角动量为0,光谱项为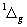 ,这两种状态都是B2的激发态。光谱项右上角的+、-号则是对应核间轴所在的平面,波函数是对称的记为+,反对称的记为-。异核双原子分子光谱项则无g,u之分。 ,这两种状态都是B2的激发态。光谱项右上角的+、-号则是对应核间轴所在的平面,波函数是对称的记为+,反对称的记为-。异核双原子分子光谱项则无g,u之分。
4.轨道能级示意图
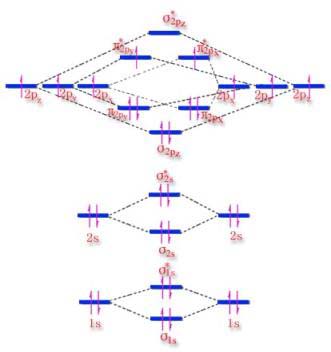
图4-3 O2分子的分子轨道能级图
|