|
例题与习题
二 .练习题(2/2)
(三)．计算题：（共65分）
1．（本题5分）8078
限制在边长为L的正方形中的N个自由电子，电子的能量为
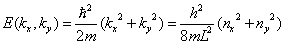
（1）求能量E到
E+dE之间的状态数（包括自旋态）
（2）求此二维系统在绝对零度的Fermi能量（
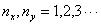）(参考答案）
解：
（1）
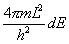
（2）
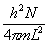
2．已知金属
Ni为A1型结构，原子间最近接触距离为249.2pm试计算：
（1）Ni立方晶胞参数
（2）金属
Ni 的密度（以g·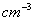 
表示）(参考答案）
解：
（1）
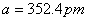
（2）
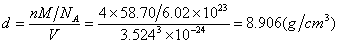
3．已知金属A1晶体按A1型堆积而成，其粉末图第二对谱线间的距离为45.3mm，所用X-射线
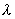=154.2pm，相机半径为28.65mm。求金属 A1晶体的晶胞参数，原子半径和晶体密度。(参考答案）
4．已知金属钛为六方最密堆积结构，金属钛原子半径为146pm，试计算理想的六方晶胞参数。(参考答案）
解：
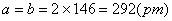
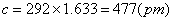
5．金属钽为立方体心结构，立方晶胞参数a=330pm，试求（110）面间距，若用
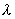为154pm的X-射线，衍射指标为220的衍射角 
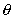的数值是多少?(参考答案）
6．金属Pd为立方面心密堆积，a=389.0，试求Pd原子之间的最短距离是多少？金属Pd的密度是多少？(参考答案）
7．证明A1型面心立方密堆积的空间利用率为74.05%。(参考答案）
解：
A1型密堆积方式ABCABC…
晶胞中4个球分数坐标为
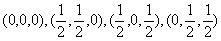。设等径圆球半径为r ，面对角线 
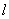=4r ，晶胞棱长a ，则
,
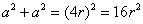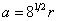
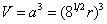
球总体积=
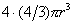
空间利用率=
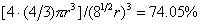
8．证明A2型体心立方密堆积的空间利用率为68.02%。(参考答案）
解：
A2型密堆积，其配位数是8，晶胞有两个等径球，分数坐标
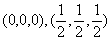,体对角线3个等径球接触，体对角线为 
。
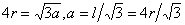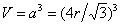
空间利用率=
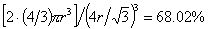
9．有一黄铜合金含Cu75%
，Zn25%（质量分数），晶体的密度为8.5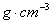 
，晶体属立方面心点阵结构，晶胞中含4个原子，相对原子质量分别为：Cu 63.5 ,Zn 65.4 。
（1）求算Cu和Zn所占原子百分数
（2）每个晶胞中含合金的质量
（3）晶胞体积多大？
（4）统计原子的原子半径多大？(参考答案）
解：（1）Cu的摩尔分数x，Zn
为1-x；63.5x:65.4(1-x)，Cu的原子百分数75.5，1-x=0.245,Zn的原子百分数24.5。
（2）
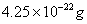
（3）
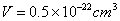
（4）
|
。
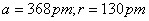
