|
第九章 离子化合物
Chapter 9. Ionic compounds
§9.1 晶格能(Lattice energy)
离子晶体是由电负性差别很大的两种或几种元素形成的化合物。一方面,由典型的金属元素,失去一个或多个电子形成正离子,另一方面由典型的非金属获得等价的电子形成负离子。正负离子由库仑力(静电力)相互结合在一起,这种化学键称离子键,库仑力与正负离子电荷成正比,与正负离子间距成反比。
一.晶格能的静电模型
我们可用晶格能来表示离子键的强弱。首先讨论晶格能的静电模型。若两个离子各带电荷q1e和q2e(视为点电荷),两者相距r,则静电库仑势
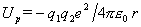
负号表示两个离子电荷符号相反,导致离子间相互吸引。在晶体中,必需考虑所有N个离子间的相互作用
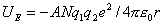
A是晶体结构类型的参数,1918年由Madelung提出,所以称Madelung常数。
1.Madelung常数
首先考虑一维晶体,图9-1表示一维无限晶体,由正负交替的点电荷(电量为e)组成,两者相隔r距离。以任意一个点为原点,它与最近邻点异号离子产生吸引能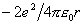 ,第二近邻是同号电荷排斥能
,第二近邻是同号电荷排斥能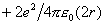 ,第三近邻又是异号电荷吸引能
,第三近邻又是异号电荷吸引能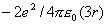 。……一系列点电荷的总静电能为
。……一系列点电荷的总静电能为
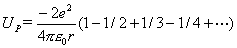
令
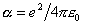 ,
, 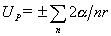 ,n=1,2,3……
,n=1,2,3……
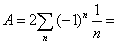 2ln(2)=1.3863,即一维结构Madelung常数为1.3863 2ln(2)=1.3863,即一维结构Madelung常数为1.3863
-∞…… - + - + - +
- + ……→∞
图9-1 一维晶体示意图
|
接下来我们讨论三维结构的Madelung常数。以NaCl构型为例:
取晶胞中的Na+作原点,6个最近邻的Cl-的静电吸引能为
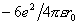 ,Na+-Cl-间距为r0,Na+第二近邻为晶胞12条棱中心位置的Na+,Na+-Na+间距为
,Na+-Cl-间距为r0,Na+第二近邻为晶胞12条棱中心位置的Na+,Na+-Na+间距为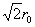 ,静电排斥能为
,静电排斥能为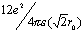 ,Na+的第三近邻为晶胞顶点的8个Cl-,静电吸引能为
,Na+的第三近邻为晶胞顶点的8个Cl-,静电吸引能为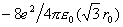 ……这样,每个Na+的库仑作用势为
……这样,每个Na+的库仑作用势为
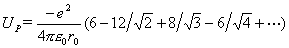
|
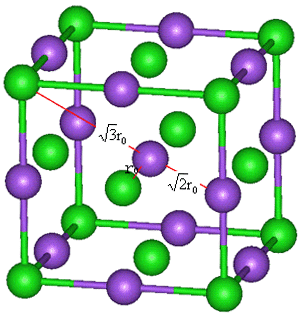
图9-2 NaCl晶体中的离子间距
|
括号内的多项式趋近于1.74756……,即NaCl型晶体的Madelung常数。
表9-1列出几种典型离子晶体的Madelung常数
表9-1
离子晶体的Madelung常数
|
构型
|
NaCl
|
CsCl
|
立方ZnS
|
六方ZnS
|
CaF2
|
TiF2
|
立方SiO2
|
|
Madelung常数
|
1.7476
|
1.7627
|
1.6407
|
1.6381
|
2.5194
|
2.3851
|
2.2011
|
2.晶格能方程
以上讨论了离子间的静电作用,晶体的总静电作用能为
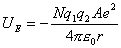
离子间相距一定距离r而不能无限接近,是因为离子间的电子云存在着斥力。Born假设,两个离子间的排斥力可用B/rn来表示,B与n是实验难以测定的常数,这样晶格能的负值可由下式给出:
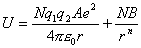
又
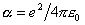

晶体在平衡态时静电作用能与排斥能达到平衡,则离子在平衡位置附近振动:
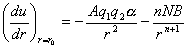
可得到
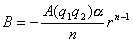 ,代入晶格能公式得:
,代入晶格能公式得:
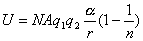
n的值可以从测定固体压缩能推出,也可以从理论上估算,在6~11之间。
|